8. 模型推断：消元法

整个概率图模型的理论可以分为三大块：模型表示（Presentation）、 模型推断（Inference）和模型学习（Learning）。 我们已经讨论完模型的表示问题， 本章开始我们讨论模型的推断问题。 图模型中的概率推断问题一般有三类，分别是

• 边缘概率（Marginal probabilities）查询。

• 条件概率（Conditional probabilities）查询。

• 最大后验概率（Maximum a posterior probabilities,MAP）查询。

其中边缘概率查询和条件概率查询其实是等价的，在计算过程中没有太大区别， 因此通常会把这两类问题合并在一起。 在概率图模型中解决概率查询问题的算法有很多， 根据是否可以得到精确结果可以划分为两大类， 精确推断算法和近似推断算法， 顾名思义，精确推断算法可以得到准确的查询概率值， 而近似推断算法只能得到近似的结果。 既然已经有精确推断算法了，为什么还要近似算法呢？ 显然，精确算法有它的局限性，不能解决所有的问题， 所以才需要通过损失精度的方法去解决所面临问题。 本章我们讨论图模型中可以精确进行概率查询的消元算法， 消元法是图模型中进行概率查询的基础算法，属于入门必须课。

图 8.1 模型推断的类型和求解算法

(8.1)\[ \begin{align}\begin{aligned}\newcommand{\indep}{\perp \! \!\! \perp} \newcommand{\notindep}{\not\! \perp \! \!\! \perp}\\\mathcal{X} \indep \mathcal{Y} \mid \mathcal{Z}\\\mathcal{X} \notindep \mathcal{Y} \mid \mathcal{Z}\\X \independent Y\\\newcommand{\nb}[1]{\text{ne}(#1)} \newcommand{\pa}[1]{\text{pa}(#1)} \newcommand{\ch}[1]{\text{ch}(#1)} \newcommand{\de}[1]{\text{de}(#1)} \newcommand{\an}[1]{\text{an}(#1)} \newcommand{\nd}[1]{\text{nd}(#1)} \newcommand{\can}[1]{\overline{\text{an}}(#1)} \newcommand{\ind}{⫫} \newcommand{\dsep}{\perp_d} \newcommand{\msep}{\perp_m}\\X \ind Y\end{aligned}\end{align} \]

8.1. 什么是模型的推断

在正式开始前，先通过一个简单例子直观的了解一下什么是模型推断。

箱子里取球的概率问题

假设我们有两个箱子分别为 \(a_1,a_2\) ，箱子中分别装有红色球和白色球。 假设 \(a_1\) 箱子中有4个红色球和6个白色球， \(a_2\) 箱子中有8个红色球和2个白色球。 此外我们有一个特殊的硬币，投放后正面向上的概率是0.6，反面向上的概率是0.4。 首先投掷硬币，然后观察硬币的朝向。 如果正面向上就从 \(a_1\) 箱子随机取出一个球，并记录球的颜色； 如果反面朝上，就从 \(a_2\) 箱子中随机取出一个球，并记录下球的颜色。 我们随机变量 \(A\) 表示从哪个箱子取球， 随机变量 \(B\) 表示取出的球的颜色。

显然随机变量 \(A\) 和 \(B\) 是两个关联的变量（不是互相独立的）， 它们的联合概率分布表示成 \(P(A,B)\)， 并且可以分解成 \(P(A)\) 和 \(P(B|A)\) 的乘积。

(8.1.29)\[P(A,B) = P(A)P(B|A)\]

可以用一个有向图来表示这个联合概率分布

图 8.1.1 随机变量A和B的有向图表示

根据题目中描述信息，可以得出随机变量 \(A\) 的概率分布 \(P(A)\) 为

(8.1.30)\[\begin{split}\begin{array}{|c|c|} \hline A& P(A) \\ \hline a_1&0.6\\ \hline a_2&0.4\\ \hline \end{array}\end{split}\]

条件概率分布 \(P(B|A)\) 的 CPT 为

(8.1.31)\[\begin{split}\begin{array}{|c|c|c|} \hline P(B|A) & A=a_1 & A=a_2 \\ \hline B=\text{红} & 0.4 & 0.8 \\ \hline B=\text{白} & 0.6 & 0.2 \\ \hline \end{array}\end{split}\]

备注

注意，公式(8.1.31) 中的每一行表示条件概率 \(P(B=b_i|A=a_i)\)， 不是联合概率 \(P(B=b_i,A=a_i)\) ， 为了区分二者，我们在变量 \(A\) 的头上加了一个横线符号 \(\bar{A}\) ，\(\bar{A}\) 表示在 \(A\) 条件下。

根据 \(P(A,B) = P(A)P(B|A)\)， 有了 \(P(A)\) 和 \(P(B|A)\) 就意味着得到了联合概率分布 \(P(A,B)\)。 但是我们并不知道随机变量 \(B\) 的概率分布 \(P(B)\) ，在联合概率分布 \(P(A,B)\) 的基础上得到随机变量 \(B\) 的概率分布 \(P(B)\) 就称为边缘概率（Marginal probability）查询， \(P(B)\) 就称为边缘概率分布。

边缘概率推断（Marginal probabilities inference）

在一个已知的联合概率分布（概率图模型）中得到部分变量的边缘概率分布， 就是边缘概率推断（Marginal probabilities inference）问题。

现在我们看下在这个例子中如何得到边缘概率分布 \(P(B)\)， 根据贝叶斯定理有

(8.1.32)\[P(A|B) = \frac{P(A)P(B|A)}{P(B)}\]

在上述贝叶斯公式中，等式右侧的分母 \(P(B)\) 就是等式右侧分子的归一化，

(8.1.33)\[P(B) = \sum_{A} P(A)P(B|A) = \sum_{A} P(A,B)\]

可以看到在联合概率分布 \(P(A,B)\) 的基础上对变量 \(A\) 进行求和就得到了 变量 \(B\) 的边缘概率分布。 你可能一时之间不是很理解，没关系，我们用上面的例子演示一遍。

公式(8.1.30) 和 公式(8.1.31) 表示了联合概率分布 \(P(A,B)\) ， 其中变量 \(B\) 有两种可能取值，分别是 红色 和 白色 。有两种情况可以得到 红色 球， 得到 红色 球概率为

(8.1.34)\[ \begin{align}\begin{aligned}P(B=\text{红}) &= P(A=a_1) P(B=\text{红} |A=a_1)+P(A=a_2) P(B=\text{红} | A=a_2)\\&= 0.6 \times 0.4+ 0.4 \times 0.8 = 0.56\end{aligned}\end{align} \]

同样有两种情况可以得到 白色 球， 得到 白色 球的概率为

(8.1.35)\[ \begin{align}\begin{aligned}P(B=\text{白}) &=P(A=a_1) P(B=\text{白} |A=a_1) + P(A=a_2) P(B=\text{白} | A=a_2)\\&= 0.6 \times 0.6 + 0.4 \times 0.2 = 0.44\end{aligned}\end{align} \]

显然合并 公式(8.1.34) 和 公式(8.1.35) 就是变量 \(B\) 的边缘概率分布。

(8.1.36)\[\begin{split}\begin{array}{|c|c|} \hline B & P(B) \\ \hline \text{红} & 0.56\\ \hline \text{白} &0.44\\ \hline \end{array}\end{split}\]

仔细观察下 公式(8.1.34) 和 公式(8.1.35) 的过程， 就是把 \(A\) 的每种可能都代入到联合概率中一次，然后累加求和的过程。 最终的结果就是在联合概率 \(P(A,B)\) 的基础上 消除 多余的变量 \(A\) ，得到剩余变量 \(B\) 的边缘概率分布， 整个过程就是把多余的变量（变量 \(A\)）进行边际化的过程。

同理我们也可以在联合概率分布 \(P(A,B)\) 的基础上推断边缘概率分布 \(P(A)\)。 虽然我们已经知道了 \(P(A)\)，但仍可以尝试着推断一下，验证下推断结果和已知的是否一致。 根据上面的经验，可以通过在 \(P(A,B)\) 的基础上对变量 \(B\) 求和得到 \(P(A)\)。

(8.1.37)\[P(A) = \sum_{B} P(A,B) = \sum_{B} P(A)P(B|A)\]

(8.1.38)\[ \begin{align}\begin{aligned}P(A=a_1) &= P(A=a_1) P(B=\text{红} |A=a_1)+P(A=a_1) P(B=\text{白} | A=a_1)\\&= 0.6 \times 0.4+ 0.6 \times 0.6 = 0.6\\P(A=a_2) &= P(A=a_2) P(B=\text{红} |A=a_2)+P(A=a_2) P(B=\text{白} | A=a_2)\\&= 0.4 \times 0.8 + 0.4 \times 0.2 = 0.4\end{aligned}\end{align} \]

\(P(A)\) 推断过程如 公式(8.1.38) 所示， 显然最后的结果和 公式(8.1.30) 是一致的。

以上就是在概率图模型中进行边缘概率查询的例子，从联合概率分布中推断出部分变量的边缘概率分布就是 边缘概率推断问题。 然而有时在进行边缘概率推断时，会面临一个特殊情况，就是部分变量存在观测值。

条件概率推断（Conditional probabilities inference）

在部分变量存在观测值的条件下，推断出图中其余某些某些变量的边缘概率分布。

条件概率推断仍然是推断出图中部分变量的边缘概率分布，所以说二者其实是等价的， 只是在具体操作时存在细微差别，我们继续以箱子取球的例子说明。

假设有个人进行了一次实验，告诉我们取到的是红色球，让我们去猜测他是从哪个箱子取出来的。 这时我们就需要根据变量 \(B\) 的观测值(球的颜色)去推断出变量 \(A`（箱子）， 也就是计算条件概率分布 :math:`P(A|B=\text{红色})\) ， 这就是典型的条件概率推断问题，已知图中部分变量的值，去推断未知变量的边缘概率分布。

图 8.1.2 灰色阴影的结点表示观测变量

图 8.1.2 表示存在观测值的有向图模型， 与 图 8.1.1 略有不同的是，我们用灰色阴影表示存在观测值的结点（变量）。 我们的任务是在联合概率分布 \(P(A,B)\) 中推断出条件概率分布 \(P(A|B=\text{红})\) 。

条件概率分布的推断同样也是建立在贝叶斯定理（推断） 的基础上的，根据贝叶斯定理（ 公式(8.1.32)）有:

(8.1.39)\[ \begin{align}\begin{aligned}P(A|B=\text{观测值}) &= \frac{P(B=\text{观测值}|A) P(A)}{P(B=\text{观测值})}\\\text{后验概率} &= \frac{\text{似然} \times \text{先验概率}}{\text{边缘概率}}\end{aligned}\end{align} \]

在贝叶斯推断中，把已知的（未取得观测样本之前的） \(P(A)\) 称为先验概率， 取得观测值后，根据观测值推断出的 \(P(A|B)\) 称为后验概率。 回到我们的例子中， 只需要按照 公式(8.1.39) 即可推断出后验条件概率分布 \(P(A|B=\text{红色})\)。

(8.1.40)\[ \begin{align}\begin{aligned}P(A=a_1|B=\text{红色}) &= \frac{P(A=a_1) P(B=\text{红} |A=a_1)}{P(B=\text{红})}\\&= \frac{0.6 \times 0.4 }{P(B=\text{红}) } = \frac{0.24 }{P(B=\text{红}) }\\P(A=a_2|B=\text{红色}) &= \frac{P(A=a_2) P(B=\text{红} |A=a_2)}{P(B=\text{红}) }\\&= \frac{0.4 \times 0.8 }{P(B=\text{红}) } = \frac{0.32 }{P(B=\text{红}) }\end{aligned}\end{align} \]

这里可以看到，条件概率的推断过程中需要用到观测样本的概率（分布部分） \(P(B=\text{红})\) ，在贝叶斯公式中，分母部分的作用就是对分子进行归一化，使其符合概率数值的范畴， 可以直接把所有分子的值相加即可。

(8.1.41)\[P(B=\text{红}) = 0.24 + 0.32 = 0.56\]

可以看到，这个值和前面（公式(8.1.36)）推断出的边缘概率分布 \(P(B)\) 是一致的。

8.2. 消元法

上一节我们用一个简单的例子为大家解释了概率图中的边缘概率推断和条件概率推断的问题， 本节我们介绍更一般的图结构上进行概率推断的算法。 模型推断的算法有很多种，整体上可以分为两大类：精确推断和近似推断。 精确推断算法，可以得出准确的结果，常见的有消元法、置信传播算法、联结树算法等。 近似推断算法，顾名思义，只能得到一个近似的结果，常见的有变分法、采样法等。 其中，消元法是最基础的方法，算法过程非常直观，并且兼容性很好， 在有向图和无向图中都可以使用， 然而消元法也有一些限制和不足，最典型的就是计算复杂度较高， 但它非常适合作为入门算法。

8.2.1. 有向图消元算法

图 8.2.1 无底色结点表示要推断的变量，浅色阴影结点是观测变量，深色阴影结点表示其它变量。

我们用一个更一般的有向图来阐述消元法的过程， 图 8.2.1 所示是一个由6个结点组成的有向图， 一般情况下，模型中的结点（变量）可以分为三类：

1. 查询变量集合，需要推断的变量集合。

2. 观测变量集合，存在观测值的变量集合。观测变量也称为证据（Evidence）变量，观测值称为证据(Evidence）。

3. 隐变量集合，既不是查询变量也不是观测变量。

我们用符号 \(V\) 表示图中全部结点的集合，\(V=\{X_1,X_2,X_3,X_4,X_5,X_6\}\)。 用符号 \(F=\{X_1\}\) 表示查询变量集合， 符号 \(E=\{X_6\}\) 表示观测变量（证据变量）集合， 符号 \(W=\{ X_2,X_3,X_4,X_5\}\) 表示隐变量集合。 此外，我们约定用大写字母 \(X\) 表示随机变量， 对应的小写字母 \(x\) 表示随机变量的一种可能取值， 用花式符号 \(\mathcal{X}\) 表示变量的取值空间，即 \(x \in \mathcal{X}\) 。 为了使算法过程描述简单些， 假设图中所有结点都是二值离散的伯努利随机变量，只有 \(0\) 或 \(1\) 两个可能的取值， 即 \(\mathcal{X}=\{0,1\}\)。 同时假设图中所有局部条件概率都是已知的， 继续用 CPT 的形式给出局部条件概率分布的内容。

(8.2.2)\[\begin{split}\begin{array}{|c|c|} \hline X_1& P(X_{1})\\ \hline 0&0.3\\ \hline 1&0.7\\ \hline \end{array}\end{split}\]

(8.2.3)\[\begin{split}\begin{array}{|c|c|c|} \hline P(X_{2}|X_1) &X_1=0 & X_1=1 \\ \hline X_2=0 & 0.4 & 0.5\\ \hline X_2=1 & 0.6 & 0.5\\ \hline \end{array}\end{split}\]

(8.2.4)\[\begin{split}\begin{array}{|c|c|c|} \hline P(X_{3}|X_1) & X_1=0 & X_1=1 \\ \hline X_3 = 0& 0.3 &0.6\\ \hline X_3 = 1& 0.7 &0.4\\ \hline \end{array}\end{split}\]

(8.2.5)\[\begin{split}\begin{array}{|c|c|c|} \hline P(X_{4}|X_2) &X_2=0& X_2=1 \\ \hline X_4=0 &0.2 &0.7\\ \hline X_4=1 &0.8 &0.3\\ \hline \end{array}\end{split}\]

(8.2.6)\[\begin{split}\begin{array}{|c|c|c|} \hline P(X_{5}|X_3) &X_3=0& X_3=1\\ \hline X_5=0& 0.7 &0.3\\ \hline X_5=1& 0.3 &0.7\\ \hline \end{array}\end{split}\]

(8.2.7)\[\begin{split}\begin{array}{|c|c|c|c|c|} \hline P(X_{6}|X_2,X_5) & X_2=0,X_5=0 & X_2=0,X_5=1 & X_2=1,X_5=0 & X_2=1,X_5=1 \\ \hline X_6=0 & 0.4 & 0.8 &0.1 & 0.3\\ \hline X_6=1 & 0.6 & 0.2 &0.9 & 0.7\\ \hline \end{array}\end{split}\]

公式(8.2.2) 到 公式(8.2.7) 就是联合概率分布 \(P(X_F,X_W,X_E)\) 的表示， 我们的任务就是在此基础上推断出条件概率分布 \(P(X_F|X_E=x_E)\)。 注意概率图模型的推断问题都是建立在图模型的结构以及概率分布已知的情况下。

在这个例子中，我们的任务是在给定 \(X_E\) 的观测值的条件下，推断出查询变量集合 \(X_F\) 的条件概率分布 \(P(X_F|X_E=x_E)\) 。 根据上一节的例子， 首先需要从联合概率分布 \(P(X_F,X_W,X_E)\) 中消除的掉隐变量（未观测到的变量）集合 \(X_W\) 得到 \(P(X_F,X_E)\)， 消除的方法就是进行求和（积分）操作。

(8.2.8)\[P(X_E,X_F) = \sum_{X_W} P(X_E,X_F,X_W)\]

然后根据贝叶斯定理，得到条件概率分布 \(P(X_F|X_E)\)

(8.2.9)\[P(X_F|X_E) = \frac{P(X_F,X_E)}{P(X_E)} = \frac{ \sum_{X_W} P(X_E,X_F,X_W) }{P(X_E)}\]

分母 \(P(X_E)\) 是对分子的归一化，可以通过分子进行累加求和得到 ，也相当于对分子进行边缘化。

(8.2.10)\[P(X_E) = \sum_{X_F} P(X_E,X_F) =\sum_{X_F} \left [ \sum_{X_W} P(X_E,X_F,X_W) \right ]\]

提示

这里重新声明一下符号的意义，使读者更容易理解后续的计算过程。 大写字母 \(P\) 表示 概率分布， 小写字母 \(p\) 表示 概率值。 大写字母 \(X\) 表示 随机变量， 小写字母 \(x\) 表示 一般变量，即数值变量，代表随机变量 \(X\) 的可能取值。 头上带有横线的小写字母 \(\bar{x}\) 表示一个已知的 定值，代表随机变量 \(X\) 某个确定的取值。

在这个例子中，假设观测变量 \(X_E=\{X_6\}\) 的观测值为 \(\{X_6=\bar{x}_6=1 \}\)， 在此基础上，推断出 \(X_1=x_1\) 的概率， 即条件概率 \(p(x_1|\bar{x}_6)\) 。

根据 公式(8.2.8)， 首先要计算边缘联合概率 \(p(x_1,\bar{x}_6)\) 。

(8.2.11)\[ \begin{align}\begin{aligned}&p(x_1,\bar{x}_6)\\&= \sum_{X_W} p(X_E=x_E,X_F=x_F,X_W)\\&= \sum_{x_2,x_3,x_4,x_5} p(x_1,x_2,x_3,x_4,x_5,\bar{x_6})\\&= \sum_{x_2,x_3,x_4,x_5} p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_4|x_2)p(x_5|x_3)p(\bar{x_6}|x_2,x_5)\\&= \sum_{x_2} \sum_{x_3} \sum_{x_4} \sum_{x_5} p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_4|x_2)p(x_5|x_3)p(\bar{x}_6|x_2,x_5)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) \sum_{x_4} p(x_4|x_2) \sum_{x_5} p(x_5|x_3)p(\bar{x}_6|x_2,x_5)\end{aligned}\end{align} \]

观察 公式(8.2.11) 发现，其中存在嵌套的求和操作。 这种情况下，需要先计算内层求和操作，再计算外层求和操作， 按照从内到外的顺序计算， 这个顺序对应消元的顺序。 为了便于大家理解，在每一个步骤中，会同时给出表格计算法和矩阵计算法， 使广大读者可以自行通过矩阵运算实现消元算法。

步骤1：消除 \(X_6\)

最内层的部分是 \(\sum_{x_5} p(x_5|x_3)p(\bar{x}_6|x_2,x_5)\) ，其中 \(\bar{x}_6\) 是观测值，是确定的已知的， 因此可以先把 \(\bar{x}_6\) 处理掉。 \(p(\bar{x}_6|x_2,x_5)\) 属于局部条件概率分布 \(P(X_6|X_2,X_5)\) ，把 \(\bar{x}_6=1\) 代入到 公式(8.2.7) ，相当于从表格中筛选出 \(X_6=1\) 的行， 得到的结果用 \(m_6(x_2,x_5)\) 表示，

(8.2.12)\[\begin{split}&m_6(x_2,x_5) \triangleq p(\bar{x}_6=1|x_2,x_5)\\\ &= \begin{array}{|c|c|c|c|c|} \hline p(x_6=1|x_2,x_5) & x_2=0,x_5=0 & x_2=0,x_5=1 & x_2=1,x_5=0 & x_2=1,x_5=1\\ \hline x_6=1 & 0.6 & 0.2 & 0.9 & 0.7 \\ \hline \end{array}\\\ &= \begin{array}{|c|c|c|} \hline x_2&x_5&m_6(x_2,x_5)\\ \hline 0&0&0.6\\ \hline 0&1&0.2\\ \hline 1&0&0.9\\ \hline 1&1&0.7\\ \hline \end{array}\end{split}\]

现在我们看下，如何用矩阵计算处理上述过程。 局部条件概率 \(p(\bar{x}_6|x_2,x_5)\) 包含三个变量， 公式(8.2.7) 可以用一个三维的矩阵来表示，矩阵的形状是 \(|X_6| \times |X_2| \times |X_5|\) 。

(8.2.13)\[\begin{split}P(X_6|X_2,X_5) \triangleq \underbrace{ \begin{bmatrix} \begin{bmatrix} 0.4 & 0.8 \\ 0.1 & 0.3 \end{bmatrix}\\ \begin{bmatrix} 0.6 & 0.2 \\ 0.9 & 0.7 \end{bmatrix} \end{bmatrix} }_{|X_6| \times |X_2| \times |X_5| }\end{split}\]

变量 \(X_6\) 是观测变量，存在观测值。 可以用一个二维矩阵表示变量的观测值， 矩阵的行表示样本，矩阵的列对应观测变量 \(|X_6|\) 的取值, 观测样本矩阵的形状为 \(\text{样本数量} \times |X_6|\) 。矩阵中第 \(i\) 行第 \(j\) 列的元素值为 \(1\) 表示第 \(i\) 条观测样本观测到变量取值为第 \(j\) 个值， 其它元素值为 \(0\) 。

(8.2.14)\[\begin{split}\text{观测样本矩阵示例：} \underbrace{\begin{bmatrix} 0 & 1 \\ .. & .. \\ 1 & 0 \\ \end{bmatrix}}_{\text{样本数量} \times |X_6|}\end{split}\]

在本例中，变量 \(X_6\) 只有 \(1\) 条观测样本且观测值为 \(\bar{x}_6=1\) ，观测矩阵表示为

(8.2.15)\[\underbrace{ \begin{bmatrix} 0 & 1 \end{bmatrix}}_{1 \times |X_6|}\]

定义 \(m_6(x_2,x_5)\) 表示消除 \(X_6\) 后得到的结果， 显然，从局部条件概率 \(p(\bar{x}_6|x_2,x_5)\) 中消除 \(x_6\) 后，得到的结果是一个关于 \(x_2\) 和 \(x_5\) 的函数信息。

(8.2.16)\[\begin{split}m_6(x_2,x_5) = \underbrace{\begin{bmatrix} 0 & 1 \end{bmatrix}\\}_{1 \times |X_6|} \cdot \underbrace{ \begin{bmatrix} \begin{bmatrix} 0.4 & 0.8 \\ 0.1 & 0.3 \end{bmatrix}\\ \begin{bmatrix} 0.6 & 0.2 \\ 0.9 & 0.7 \end{bmatrix} \end{bmatrix} }_{|X_6| \times |X_2| \times |X_5| } = \underbrace{\begin{bmatrix} 0.6 & 0.2\\ 0.9 &0.7 \end{bmatrix} }_{|X_2| \times |X_5|}\end{split}\]

符号 \(\cdot\) 表示矩阵的內积乘法，內积的运算过程是行列相乘然后求和，正好对应着消元操作。 \(m_i\) 函数只是表示去掉结点（变量） \(X_i\) 之后的结果信息，并没有概率意义，不需要符合概率的约束(和为1)。

步骤2：消除 \(X_5\)

然后定义 \(m_5(x_2,x_3) = \sum_{x_5} p(x_5|x_3)m_6(x_2,x_5)\) ，这一步把 \(X_5\) 从图中消除掉。

先计算 \(p(x_5|x_3)m_6(x_2,x_5)\) ，

(8.2.17)\[\begin{split} p(x_5|x_3) m_6(x_2,x_5) &= \begin{array}{|c|c|c|} \hline x_3 &x_5& p(x_5|x_3) \\ \hline 0&0&0.7\\ 0&1&0.3\\ \hline 1&0&0.3\\ 1&1&0.7\\ \hline \end{array} \times \begin{array}{|c|c|c|} \hline x_2& x_5& m_6(x_2,x_5) \\ \hline 0&0&0.6\\ \hline 0&1&0.2\\ \hline 1&0&0.9\\ \hline 1&1&0.7\\ \hline \end{array} \\\ &= \begin{array}{|c|c|c|c|} \hline x_2&x_5&x_3& p(x_5|x_3) m_6(x_2,x_5) \\\hline 0&0&0& 0.6\times0.7=0.42 \\\hline 0&0&1& 0.6\times0.3=0.18 \\\hline 0&1&0& 0.2\times0.3=0.06 \\\hline 0&1&1& 0.2\times0.7=0.14 \\\hline 1&0&0& 0.9\times0.7=0.63 \\\hline 1&0&1& 0.9\times0.3=0.27 \\\hline 1&1&0& 0.7\times0.3=0.21 \\\hline 1&1&1& 0.7\times0.7=0.49 \\\hline \end{array}\end{split}\]

再消除 \(x_5\) 。消除方法就是 \(x_2\) 和 \(x_3\) 维持不变， 对应的 \(x_5=0\) 和 \(x_5=1\) 的两行求和。

(8.2.18)\[\begin{split}m_5(x_2,x_3) = \sum_{x_5} p(x_5|x_3) m_6(x_2,x_5) = \begin{array}{|c|c|c|} \hline x_2&x_3& m_5(x_2,x_3) \\\hline 0&0& 0.42+0.06=0.48\\\hline 0&1& 0.18+0.14=0.32 \\\hline 1&0& 0.63+0.21=0.84\\\hline 1&1& 0.27+0.49=0.76 \\\hline \end{array}\end{split}\]

同样，这个过程可以通过矩阵运算得到

(8.2.19)\[\begin{split}m_5(x_2,x_3) &= \sum_{x_5} m_6(x_2,x_5) p(x_5|x_3)\\\ &= \underbrace{\begin{bmatrix} 0.6 & 0.2\\ 0.9 &0.7 \end{bmatrix} }_{|X_2| \times |X_5|} \cdot \underbrace{\begin{bmatrix} 0.7 & 0.3\\ 0.3 &0.7 \end{bmatrix} }_{|X_5| \times |X_3|}\\\ &=\underbrace{\begin{bmatrix} 0.6 \times 0.7+ 0.2 \times 0.3 & 0.6 \times 0.3 + 0.2 \times 0.7\\ 0.9 \times 0.7+ 0.7 \times 0.3 & 0.9 \times 0.3 + 0.7 \times 0.7 \\ \end{bmatrix} }_{|X_2| \times |X_3|} \\\ &=\underbrace{\begin{bmatrix} 0.48 & 0.32 \\ 0.84 & 0.76 \\ \end{bmatrix} }_{|X_2| \times |X_3|}\end{split}\]

把 \(m_5(x_2,x_3)\) 代入到 公式(8.2.11) 可得：

(8.2.20)\[ \begin{align}\begin{aligned}p(x_1,\bar{x}_6) &= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) \sum_{x_4} p(x_4|x_2) \sum_{x_5} p(x_5|x_3)p(\bar{x}_6|x_2,x_5)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) \sum_{x_4} p(x_4|x_2) m_5(x_2,x_3)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) m_5(x_2,x_3) \sum_{x_4} p(x_4|x_2)\end{aligned}\end{align} \]

上式计算过程中，由于 \(m_5(x_2,x_3)\) 与 \(x_4\) 无关（第2行），因此可以把 \(m_5(x_2,x_3)\) 移到 \(\sum_{x_4} p(x_4|x_2) m_5(x_2,x_3)\) 的上一层去（第3行)。

步骤3：消除 \(X_4\)

接下来继续计算 \(\sum_{x_4} p(x_4|x_2)\) 消除掉变量 \(X_4\) ，定义 \(m_4(x_2) = \sum_{x_4} p(x_4|x_2)\) ，则有

(8.2.21)\[\begin{split}m_4(x_2)=\sum_{x_4} p(x_4|x_2) = \sum_{x_4} \begin{array}{|c|c|c|} \hline x_2&x_4& p(x_4|x_2) \\ \hline 0&0&0.2\\ 0&1&0.8\\ \hline 1&0&0.7\\ 1&1&0.3\\ \hline \end{array} = \begin{array}{|c|c|} \hline x_2& m_4(x_2) \\ \hline 0&1\\ \hline 1&1\\ \hline \end{array}\end{split}\]

\(X_4\) 和 \(X_6\) 一样是叶子结点， 不同的是，\(X_4\) 没有观测值。 对于没有观测样本的叶子结点，需要用一个全为 \(1\) 的矩阵表示”观测”， 全为 \(1\) 意味不确定取什么值，没有观测到。 \(X_4\) 有两种可能取值， 因此是一个形状为 \(1 \times 2\) 的全 \(1\) 矩阵： \([1,\ 1]\)。

(8.2.22)\[\begin{split}m_4(x_2) &=\sum_{x_4} p(x_4|x_2) \\\ &= \underbrace{\begin{bmatrix} 1 & 1 \end{bmatrix}}_{1\times |X_4|} \underbrace{\begin{bmatrix} 0.2 & 0.7\\ 0.8 & 0.3 \end{bmatrix} }_{|X_4| \times |X_2|}\\\ &= \underbrace{\begin{bmatrix} 1 & 1 \end{bmatrix} }_{1 \times |X_2|}\end{split}\]

将 \(m_4(x_2)\) 代入到 公式(8.2.20) ：

(8.2.23)\[ \begin{align}\begin{aligned}p(x_1,\bar{x}_6) &= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) m_4(x_2) m_5(x_2,x_3)\\&= p(x_1) \sum_{x_2} m_4(x_2) p(x_2|x_1) \sum_{x_3} m_5(x_2,x_3) p(x_3|x_1)\end{aligned}\end{align} \]

步骤4：消除 \(X_3\)

类似的，定义 \(m_3(x_2,x_1)=\sum_{x_3} m_5(x_2,x_3) p(x_3|x_1)\) ，表格的计算过程为

(8.2.24)\[\begin{split}p(x_3|x_1) m_5(x_2,x_3) &= \begin{array}{|c|c|c|} \hline x_1& x_3 & p(x_3|x_1) \\ \hline 0&0&0.3\\ 0&1&0.7\\ \hline 1&0&0.6\\ 1&1&0.4\\ \hline \end{array} \times \begin{array}{|c|c|c|} \hline x_2&x_3& m_5(x_2,x_3) \\ \hline 0&0&0.48\\ \hline 0&1&0.32\\\hline 1&0&0.84\\\hline 1&1&0.76\\\hline \end{array} \\\ &= \begin{array}{|c|c|c|c|} \hline x_1& x_2& x_3& p(x_3|x_1) m_5(x_2,x_3) \\ \hline 0&0&0& 0.3\times 0.48=0.144 \\\hline 0&0&1& 0.7\times 0.32=0.224 \\\hline 0&1&0& 0.3\times 0.84=0.252 \\\hline 0&1&1& 0.7\times 0.76=0.532 \\\hline 1&0&0& 0.6\times 0.48=0.288 \\\hline 1&0&1& 0.4\times 0.32=0.128\\\hline 1&1&0& 0.6\times 0.84=0.504\\\hline 1&1&1& 0.4\times 0.76=0.304\\\hline \end{array}\end{split}\]

(8.2.25)\[\begin{split}m_3(x_2,x_1) &=\sum_{x_3} m_5(x_2,x_3) p(x_3|x_1) \\\ &= \begin{array}{|c|c|c|} \hline x_1&x_2& m_3(x_2,x_1) \\ \hline 0&0& 0.144+0.224=0.368\\\hline 0&1& 0.252+0.532=0.784\\\hline 1&0& 0.288+0.128=0.416 \\\hline 1&1& 0.504+0.304=0.808 \\\hline \end{array}\end{split}\]

矩阵的计算过程为

(8.2.26)\[\begin{split}m_3(x_2,x_1) &= \sum_{x_3} m_5(x_2,x_3) p(x_3|x_1)\\\ &= \underbrace{\begin{bmatrix} 0.48 & 0.32 \\ 0.84 & 0.76 \\ \end{bmatrix} }_{|X_2| \times |X_3|} \cdot \underbrace{\begin{bmatrix} 0.3 & 0.6 \\ 0.7 & 0.4 \\ \end{bmatrix} }_{|X_3| \times |X_1|}\\\ &=\underbrace{\begin{bmatrix} 0.48 \times 0.3 + 0.32 \times 0.7 & 0.48 \times 0.6 + 0.32 \times 0.4 \\ 0.84 \times 0.3 + 0.76 \times 0.7 & 0.84 \times 0.6 + 0.76 \times 0.4 \end{bmatrix} }_{|X_2| \times |X_1|} \\\ &=\underbrace{\begin{bmatrix} 0.368 & 0.416 \\ 0.784 & 0.808 \end{bmatrix} }_{|X_2| \times |X_1|}\end{split}\]

将 \(m_3(x_2,x_1)\) 代入 公式(8.2.23) 可得，

(8.2.27)\[p(x_1,\bar{x}_6) =p(x_1) \sum_{x_2} p(x_2|x_1) m_4(x_2) m_3(x_2,x_1)\]

步骤5：消除 \(X_2\)

定义 \(m_2(x_1)=\sum_{x_2} p(x_2|x_1) m_4(x_2) m_3(x_2,x_1)\) ，表格计算过程为

(8.2.28)\[\begin{split}m_4(x_2) m_3(x_1,x_2) &= \begin{array}{|c|c|} \hline x_2& m_4(x_2) \\ \hline 0&1\\ \hline 1&1\\ \hline \end{array} \times \begin{array}{|c|c|c|} \hline x_1&x_2&m_3(x_1,x_2) \\ \hline 0&0& 0.368\\\hline 0&1& 0.784\\\hline 1&0& 0.416 \\\hline 1&1& 0.808 \\\hline \end{array} \\\ &= \begin{array}{|c|c|c|} \hline x_1&x_2& m_4(x_2) m_3(x_1,x_2) \\ \hline 0&0& 0.368\\\hline 0&1& 0.784\\\hline 1&0& 0.416 \\\hline 1&1& 0.808 \\\hline \end{array}\end{split}\]

(8.2.29)\[\begin{split}p(x_2|x_1) [m_4(x_2) m_3(x_1,x_2)] &= \begin{array}{|c|c|c|} \hline x_1&x_2& p(x_2|x_1) \\ \hline 0&0&0.4\\ 0&1&0.6\\ \hline 1&0&0.5\\ 1&1&0.5\\ \hline \end{array} \times \begin{array}{|c|c|c|} \hline x_1&x_2& m_4(x_2) m_3(x_1,x_2) \\ \hline 0&0& 0.368\\\hline 0&1& 0.784\\\hline 1&0& 0.416 \\\hline 1&1& 0.808 \\\hline \end{array} \\\ &= \begin{array}{|c|c|c|} \hline x_1&x_2&message\\ \hline 0&0& 0.4\times 0.368=0.1472 \\\hline 0&1& 0.6\times 0.784=0.4704\\\hline 1&0& 0.5\times 0.416=0.208 \\\hline 1&1& 0.5\times 0.808=0.404 \\\hline \end{array}\end{split}\]

(8.2.30)\[\begin{split}m_2(x_1) &=\sum_{x_2} p(x_2|x_1) m_4(x_2) m_3(x_1,x_2) \\\ &= \begin{array}{|c|c|c|} \hline x_1&message\\ \hline 0& 0.1472+0.4704=0.6176\\\hline 1& 0.208 + 0.404=0.612 \\\hline \end{array}\end{split}\]

矩阵的计算过程为

(8.2.31)\[\begin{split}m_2(x_1) &=\sum_{x_2} m_4(x_2) p(x_2|x_1) m_3(x_2,x_1) \\\ &=\underbrace{\begin{bmatrix}1 & 1\end{bmatrix}}_{1 \times |X_2|} \cdot \left [ \underbrace{\begin{bmatrix}0.4 & 0.5 \\0.6 &0.5 \end{bmatrix}}_{|X_2| \times |X_1|} \odot \underbrace{\begin{bmatrix} 0.368 & 0.416 \\ 0.784 & 0.808 \end{bmatrix} }_{|X_2| \times |X_1|} \right ] \\\ &=\underbrace{\begin{bmatrix}1 & 1\end{bmatrix}}_{1 \times |X_2|} \cdot \underbrace{\begin{bmatrix} 0.4 \times 0.368 & 0.5 \times 0.416 \\ 0.6 \times 0.784 & 0.5 \times 0.808 \end{bmatrix} }_{|X_2| \times |X_1|} \\\ &=\underbrace{\begin{bmatrix}1 & 1\end{bmatrix}}_{1 \times |X_2|} \cdot \underbrace{\begin{bmatrix} 0.1472 & 0.208 \\ 0.4704 & 0.404 \end{bmatrix} }_{|X_2| \times |X_1|} \\\ &=\begin{bmatrix} 0.6176 & 0.612 \end{bmatrix}\end{split}\]

这一步稍微复杂些，\(p(x_2|x_1)\) 和 \(m_3(x_2,x_1)\) 都包含 \(x_1,x_2\) 的信息，需要先把两部分合并，然后再消除 \(x_2\)。 符号 \(\odot\) 表元矩阵的元素乘法，即两个矩阵对应位置相乘得到新的矩阵，没有求和操作， 这个运算对应着合并操作。 合并之后的信息再和 \(m_4(x_2)\) 进行內积乘法操作消除 \(x_2\) 。

步骤6：得到 \(p(x_1,\bar{x}_6)\)

将 \(m_2(x_1)\) 代入到 公式(8.2.27) 可得

(8.2.32)\[\begin{split}p(x_1,\bar{x}_6) &= p(x_1) \sum_{x_2} p(x_2|x_1) m_4(x_2) m_3(x_1,x_2)\\\ &= p(x_1) m_2(x_1) \\\ &= \begin{array}{|c|c|} \hline x_1& p(x_1) \\ \hline 0&0.3\\ \hline 1&0.7\\ \hline \end{array} \times \begin{array}{|c|c|c|} \hline x_1& m_2(x_1) \\ \hline 0& 0.6176\\\hline 1& 0.612 \\\hline \end{array} \\\ &= \begin{array}{|c|c|c|} \hline x_1 & p(x_1,\bar{x}_6)\\ \hline 0& 0.3\times0.6176 =0.18528 \\\hline 1& 0.7\times0.612 =0.4284 \\\hline \end{array}\end{split}\]

对应的矩阵操作为

(8.2.33)\[\begin{split} p(x_1,\bar{x}_6) &= p(x_1) m_2(x_1) \\\ &= \begin{bmatrix} 0.3 & 0.7 \end{bmatrix} \odot \begin{bmatrix} 0.6176 & 0.612 \end{bmatrix} \\\ &= \begin{bmatrix} 0.3 \times 0.6176 & 0.7 \times 0.612 \end{bmatrix}\\\ &=\begin{bmatrix} 0.18528 & 0.4284 \end{bmatrix}\end{split}\]

至此，我们得到了 \(p(x_1,\bar{x}_6)\)， 整个过程就是一个消除隐变量集合 \(X_W=\{X_2,X_3,X_4,X_5 \}\) 的过程， 并且限定观测变量 \(X_6\) 为观测值 \(\bar{x}_6=1\)。

重新整理一下整个计算过程

(8.2.34)\[ \begin{align}\begin{aligned}p(x_1,\bar{x}_6) &= \sum_{x_2,x_3,x_4,x_5} p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_4|x_2)p(x_5|x_3)p(\bar{x}_6|x_2,x_5)\\&= \sum_{x_2} \sum_{x_3} \sum_{x_4} \sum_{x_5} p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_4|x_2)p(x_5|x_3)p(\bar{x}_6|x_2,x_5)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) \sum_{x_4} p(x_4|x_2) \sum_{x_5} p(x_5|x_3)p(\bar{x}_6|x_2,x_5)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) \sum_{x_4} p(x_4|x_2) m_5(x_2,x_3)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) m_5(x_2,x_3) \sum_{x_4} p(x_4|x_2)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) \sum_{x_3} p(x_3|x_1) m_5(x_2,x_3) m_4(x_2)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) m_4(x_2) \sum_{x_3} p(x_3|x_1) m_5(x_2,x_3)\\&= p(x_1) \sum_{x_2} p(x_2|x_1) m_4(x_2) m_3(x_1,x_2)\\&= p(x_1)m_2(x_1)\end{aligned}\end{align} \]

需要注意的时， \(p(x_1,\bar{x}_6)\) 并不是一个概率分布，也不是一个概率值。 根据 公式(8.2.9) 和 公式(8.2.10) ，还需要计算出观测样本的边缘概率 \(p(\bar{x}_6)\)

(8.2.35)\[p(\bar{x}_6=1) = \sum_{x_1} p(x_1,\bar{x}_6) = \sum_{x_1}p(x_1)m_2(x_1) = 0.18528+0.4284=0.61368\]

然后根据 公式(8.2.9) 计算出条件概率 \(p(x_1|\bar{x}_6=1)\)

(8.2.36)\[\begin{split}p(x_1|\bar{x}_6=1) &= \frac{p(x_1)m_2(x_1)}{\sum_{x_1}p(x_1)m_2(x_1)} \\\ &=\frac{p(x_1)m_2(x_1)}{p(\bar{x}_6=1)} \\\ &= \begin{array}{|c|c|c|} \hline x_1& p(x_1|\bar{x}_6=1) \\ \hline 0& 0.18528/0.61368 \approx 0.3 \\\hline 1& 0.4284/0.61368 \approx 0.7 \\\hline \end{array}\end{split}\]

\(p(x_1,\bar{x}_6)\) 相当于是未归一化的条件概率 \(p(x_1|\bar{x}_6=1)\) ， 通过除以归一化常量 \(p(\bar{x}_6=1)\) 计算出条件概率 \(p(x_1|\bar{x}_6)\) 。 可以看到这个结果和我们预先设定的 \(P(X_1)\) (公式(8.2.2))几乎是一样的， 通常把基于观测样本（证据）条件下的条件概率称为后验概率，所谓的”后验”就是指：在有了观测样本（证据）之后。 因此，图模型中的条件概率查询经常也称为后验概率查询。

最后总结

至此，我们通过一个具体的例子演示了有向图消元法的计算过程，消元法是概率图模型进行推断的直接算法，是一种精确的推断算法。 但是其有个明显的缺点就是，每一次概率查询(条件概率、边缘概率推断)都需要执行一次上述过程，比如，如果我们想要查询条件概率 \(p(x_1|\bar{x}_6=0),p(x_1|\bar{x}_4),\ldots\) 等等，都需要分别执行一次上述过程，计算复杂度非常高。 在有向图中，变量消除的顺序是和图形结构（求和符号的嵌套结构）有关的， 按照特定的顺序进行处理是有利于简化计算的。

最后总结下条件概率 \(P(X_F| X_E=x_e)\) 的推断过程，

1. 根据贝叶斯定理列出查询变量 \(X_F\) 的条件概率。

(8.2.37)\[P(X_F|X_E=x_E) = \frac{P(X_F,X_E=x_E)}{P(X_E=x_E)}\]

2. 计算分子。通过边际化(marginalization)的方法， 消除概率图中联合概率分布 \(P(X_F,X_E,X_W)\) 中的隐变量集合 \(X_W\) ， 得到观测变量和查询变量的联合分布 \(P(X_F,X_E=x_E)\) 。

   (8.2.38)\[P(X_F,X_E=x_E) = \sum_{X_W} P(X_F,X_E,X_W)\]

3. 计算分母。边际化分子求得。

   (8.2.39)\[P(X_E=x_E) = \sum_{X_F} P(X_F,X_E=x_E)\]

4. 得到后验条件概率查询。

   (8.2.40)\[P(X_F| X_E=x_e) = \frac{P(X_F,X_E=x_E)}{P(X_E=x_E)}\]

显然，在推断过程中一个很重要的工作就是对联合概率分布进行边际化，以求的部分变量子集的边缘概率分布。 所以概率模型推断的核心就是边际化算法，而边际化最直接的算法就是 消元法 。 在进行变量消除(消元)处理时，离散变量概率分布求和，连续值变量概率密度函数求积分； 对于观测变量，只需要把求和(积分)操作替换成取观测值时即可。

提示

如果有多次观测（样本），则其中的似然部分就是连乘式(全部观测值同时发生):

(8.2.41)\[P(A|B=\text{\{观测值集合\}}) = \frac{ \left [ \prod_i^N P_i(B=\text{观测值}_i|A) \right ] P(A)}{P(B=\text{\{观测值集合\}})}\]

8.2.2. 条件概率和边缘概率

为了能更直观的解释消元法，这里我们通过一些定义把条件变量取定值的操作也转化成求和操作， 通过这样的转化可以令条件变量和边际化消除变量具有相同的操作，更容易理解和操作。

假设 \(X_i\) 是证据（观测）变量，其观测值是 \(\bar{x}_i\) 。 我们定义一个 证据势函数(evidence potential) ， \(\delta(x_i,\bar{x}_i)\) ， 当 \(x_i=\bar{x}_i\) 成立时这个函数值为1，否则为0。 通过这个函数我们可以把推断过程中对证据变量 \(\mathrm{x}_i\) 的限制约束 (取值为 \(\bar{x}_i\) ) 操作转化成求和操作。 函数 \(g(x_i)\) 表示变量 \(\mathrm{x}_i\) 的一个函数，比如在上面的例子中 \(g(x_6)=p(x_6|x_2,x_5)\) ，通过下面的转换可以把 \(g(\bar{x}_6)=p(\bar{x}_6|x_2,x_5)\) 转换成等价的求和操作。

(8.2.42)\[g(\bar{x}_i)=\sum_{x_i} g(x_i) \delta(x_i,\bar{x}_i) = \sum_{x_i} p(x_6|x_2,x_5) \delta(x_i,\bar{x}_i)\]

这样在执行消元推断时，对于条件(证据)变量的限制约束操作转化为一个求和操作，二者的值是等价， 这样在上面的例子中就可以额外定义出 \(m_6(x_2,x_5)\) 。

(8.2.43)\[m_6(x_2,x_5) = \sum_{x_6} p(x_6|x_2,x_5) \delta(x_6,\bar{x}_6) = p(\bar{x}_6|x_2,x_5)\]

更一般的，我们可以扩展到多个条件变量的情形，我们用E表示条件变量集合，对于特定的条件(观测、证据)值 \(\bar{x}_E\) ，我们想要计算 \(p(x_F|\bar{x}_E)\) 。这时我们定义一个 整体证据势函数(total evidence potential) ：

(8.2.44)\[\delta(x_E,\bar{x}_E) \triangleq \prod_{i\in E} \delta(x_i,\bar{x}_i)\]

只有当 \(x_E=\bar{x}_E\) 成立时，这个函数为1，否则为0。通过这个势函数，我们可以把条件概率 \(p(x_F|\bar{x}_E)\) 的分子分母都表示成求和的形式，分母其实就是分子的归一化，是在分子的基础上进行求和。

(8.2.45)\[ \begin{align}\begin{aligned}p(x_F,\bar{x}_E) = \sum_{x_E} p(x_F,x_E)\delta(x_E,\bar{x}_E)\\p(\bar{x}_E) = \sum_{x_F} \sum_{x_E} p(x_F,x_E)\delta(x_E,\bar{x}_E)\end{aligned}\end{align} \]

条件概率 \(p(x_F|\bar{x}_E)\) 的计算公式为：

(8.2.46)\[ \begin{align}\begin{aligned}p(x_F|\bar{x}_E) &= \frac{p(x_F,\bar{x}_E)}{p(\bar{x}_E)}\\&= \frac{\sum_{x_E} p(x_F,x_E)\delta(x_E,\bar{x}_E)}{\sum_{x_F} \sum_{x_E} p(x_F,x_E)\delta(x_E,\bar{x}_E)}\end{aligned}\end{align} \]

条件概率 \(p(x_F|\bar{x}_E)\) 的分母 \(p(\bar{x}_E)\) 是其分子 \(p(x_F,\bar{x}_E)\) 的累加求和， 也就是说其实只要计算出分子部分，分母就自然得到了，从某种角度上讲只要计算出 \(p(x_F,\bar{x}_E)\) 就相当于计算出 条件概率 \(p(x_F|\bar{x}_E)\) ，那么我们可以把 \(p(x_F,\bar{x}_E)\) 看成是条件概率令一种表示。 然而 \(p(x_F,\bar{x}_E)\) 本身又是在边缘概率 \(p(x_F,x_E)\) 的基础上加了一个证据势函数 \(p(x_F,\bar{x}_E)=p(x_F,x_E)\delta(x_E,\bar{x}_E)\) 。我们可以用不加修改的消元法计算 \(p(x_F,x_E)\) 和 \(p(x_F,\bar{x}_E)\) ，本质上就是模型的条件概率和边缘概率的推断问题可以看成是等价的。 两者都是进行边际化消除，计算逻辑是一样的，不同的是 \(p(x_F,\bar{x}_E)\) 多了一个证据势函数 \(\delta(x_E,\bar{x}_E)\) 。

通过引入证据势函数，我们把条件变量的值限定操作转换成了求和消除操作，条件变量可以和其他被边缘化消除的变量在操作上同等看待， 这样一来在图模型上进行条件概率查询也可以看做是进行边缘概率查询，因为两者在计算上是等价的。 也就是说我们可以把 \(p(x_F|\bar{x}_E)\) 和 \(p(x_F,x_E)\) 都当成是在求”边缘概率”， 在图模型的推断算法的讨论中，我们将不再区分两者，都会按照边缘概率查询来讨论。 这样的方式同样适用于无向图，对于证据变量集合E，为其中每个结点的局部势函数 \(\psi_i(x_i)\) 乘上 \(\delta(x_i,\bar{x}_i)\) 。

(8.2.47)\[\psi_i^E (x_i) \triangleq \psi_i(x_i)\delta(x_i,\bar{x}_i) ,i \in E\]

一个包含证据(观测值)值的有向图的条件概率，可以用的联合（边缘）概率的形式表示，其中E表示证据变量集合：

(8.2.48)\[p^E(x) \triangleq p(x) \delta (x_E,\bar{x}_E)\]

对于无向图可以有同样的定义：

(8.2.49)\[p^E(x) \triangleq \frac{1}{Z} \prod_{C \in \mathcal{C}} \psi^E_{\mathrm{x}_C} (x_C)\]

这个算法执行过程中的每一步都是在一个因子函数乘积上执行一个求和消元的过程， 这些因子函数可以是局部条件概率 \(p(x_i|x_{\pi_i})\) 、证据势函数 \(\delta(x_i,\bar{x}_i)\) 、中间信息因子 \(m_i(x_{S_i})\) 。所有的这些函数都是定义在局部结点子集上的，这里统一用 “势函数(potential function)” 表示。 所以消元算法其实是一个在势函数的乘积上面通过求和消除变量的过程。

我们整理一下有向图中消元算法的伪代码过程：

消元整体过程( \(\mathcal{G},E,F\) )

过程1： 初始化图和查询变量( \(\mathcal{G},F\) )

过程2：引入证据( \(E\) )

过程3：更新( \(\mathcal{G}\) )

过程4：归一化查询变量(F)

过程1. 初始化图和查询变量( \(\mathcal{G},F\) )

选择一个消元的顺序 \(I\) ，F 变量排在最后。

foreach \(\mathrm{x}_i\) in \(\mathcal{V}\) :

把 \(p(x_i|x_{\pi_i})\) 放到激活列表中 // 生成联合概率因子分解的过程

end for

过程2. 引入证据( \(E\) )

foreach i in E:

把 \(\delta(x_i,\bar{x}_i)\) 加入到激活列表中

end for

过程3：更新( \(\mathcal{G}\) )

foreach i in \(I\) :

从激活列表中找到所有包含 \(x_i\) 的势函数从激活列表中去掉这下势函数

令 \(\phi_i(x_{T_i})\) 表示这些势函数的乘积

令 \(m_i(x_{S_i})=\sum_{x_i} \phi_i(x_{T_i})\)

将 \(m_i(x_{S_i})\) 加入到激活列表中

end for

过程4：归一化查询变量(F)

\(p(x_F|\bar{x}_E) \leftarrow \frac{\phi_F(x_F)}{\sum_{x_F} \phi_F(x_F)}\)

注意，在上述伪代码流程中我们定义了符号 \(T_i=\{i\}\cup S_i\) ，表示的是求和子项 \(\sum_{x_i}\) 中包含的全部结点子集。当消元过程执行到只剩下查询变量 \(\mathrm{x}_F\) 时算法结束，这时我们就得到了未归一化的 “条件概率” \(p(x_F,\bar{x}_E)\) ，通过在其上面对 \(x_F\) 求和可以得到归一化因子 \(p(\bar{x}_E)\) 。 让我们回到上面的例子中，按照伪代码的过程阐述一遍。

过程1，初始化图和查询变量。 首先我们确定证据结点 \(\mathrm{x}_6\) ，查询结点是 \(\mathrm{x}_1\) 。 选定消元顺序 \(I=(6,5,4,3,2,1)\) ，其中查询结点排在最后面。 然后把所有局部条件概率放到激活列表中 \(\{p(x_1),p(x_2|x_1),p(x_3|x_1),p(x_4|x_2),p(x_5|x_3),p(x_6|x_2,x_5)\}\) 。

过程2. 引入证据。 把证据势函数 \(\delta (x_6,\bar{x}_6)\) 追加到激活列表中

(8.2.50)\[\{ p(x_1),p(x_2|x_1),p(x_3|x_1),p(x_4|x_2),p(x_5|x_3),p(x_6|x_2,x_5),\delta(x_6,\bar{x}_6) \}\]

过程3：更新。

首先消除结点 \(\mathrm{x}_6\) ，激活列表中包含变量 \(\mathrm{x}_6\) 的”势函数(potential function)”有 \(p(x_6|x_2,x_5)\) 和 \(\delta(x_6,\bar{x}_6)\) ，所以我们有 \(\phi_6(x_2,x_5,x_6)=p(x_6|x_2,x_5)\delta(x_6,\bar{x}_6)\) ，对 \(x_6\) 进行求和得到 \(m_6(x_2,x_5)=p(\bar{x}_6|x_2,x_5)\) 。把这个新的势函数加入到激活列表中，并且从激活列表中移除 \(p(x_6|x_2,x_5)\) 和 \(\delta(x_6,\bar{x}_6)\) 。至此，我们就完成了证据的引入，把 \(p(x_6|x_2,x_5)\) 限定为 \(\bar{x}_6\) 。此时激活列表为 \(\{p(x_1),p(x_2|x_1),p(x_3|x_1),p(x_4|x_2),p(x_5|x_3),m_6(x_2,x_5)\}\)

现在开始消除变量 \(\mathrm{x}_5\) ，激活列表中包含变量 \(\mathrm{x}_5\) 的势函数有 \(p(x_5|x_3)\) 和 \(m_6(x_2,x_5)\) ，移除它们，然后定义 \(\phi_5(x_2,x_3,x_5)=p(x_5|x_3)m_6(x_2,x_5)\) ，对 \(\mathrm{x}_5\) 进行求和得到 \(m_5(x_2,x_3)\) ，加入到激活列表中。此时，激活列表为 \(\{p(x_1),p(x_2|x_1),p(x_3|x_1),p(x_4|x_2),m_5(x_2,x_3)\}\) 。

现在开始消除变量 \(\mathrm{x}_4\) ，激活列表中包含变量 \(\mathrm{x}_4\) 的势函数有 \(p(x_4|x_2)\) ，移除它，然后定义 \(\phi_4(x_2,x_4)=p(x_4|x_2)\) ，对 \(\mathrm{x}_4\) 进行求和得到 \(m_4(x_2)\) ，加入到激活列表中。此时，激活列表为 \(\{p(x_1),p(x_2|x_1),p(x_3|x_1),m_4(x_2),m_5(x_2,x_3)\}\) 。

现在开始消除变量 \(\mathrm{x}_3\) ，激活列表中包含变量 \(\mathrm{x}_3\) 的势函数有 \(p(x_3|x_1)\) 和 \(m_5(x_2,x_3)\) ，移除它们，然后定义 \(\phi_3(x_1,x_2,x_3)=p(x_3|x_1)m_5(x_2,x_3)\) ，对 \(\mathrm{x}_3\) 进行求和得到 \(m_3(x_1,x_2)\) ，加入到激活列表中。此时，激活列表为 \(\{p(x_1),p(x_2|x_1),m_4(x_2),m_3(x_1,x_2)\}\) 。

现在开始消除变量 \(\mathrm{x}_2\) ，激活列表中包含变量 \(\mathrm{x}_2\) 的势函数有 \(p(x_2|x_1),m_4(x_2),m_3(x_1,x_2)\) ，移除它们，然后定义 \(\phi_2(x_1,x_2)=p(x_2|x_1),m_4(x_2),m_3(x_1,x_2)\) ，对 \(\mathrm{x}_2\) 进行求和得到 \(m_2(x_1)\) ，加入到激活列表中。此时，激活列表为 \(\{p(x_1),m_2(x_1)\}\) 。

过程4：归一化查询变量。

现在我们得到了 \(\phi_1(x_1)=p(x_1)m_2(x_1)\) ，这其实就是”未归一化的条件概率” \(p(x_1,\bar{x}_6)\) ， 在其基础上消除 \(x_1\) 得到 \(m_1=\sum_{x_1} \phi_1(x_1)\) 就是归一化因子 \(p(\bar{x}_6)\) 。

8.2.3. 无向图的消元法

有向图的消元算法同样也适用于无向图，并不需要过多改变。唯一的变化就是激活列表中有向图的局部条件概率变成无向图的势函数 \(\{\psi_{\mathrm{x}_C}(x_C)\}\)。 让我们考虑一个无向图的示例 ，这个无向图是上节的有向图转化而来。

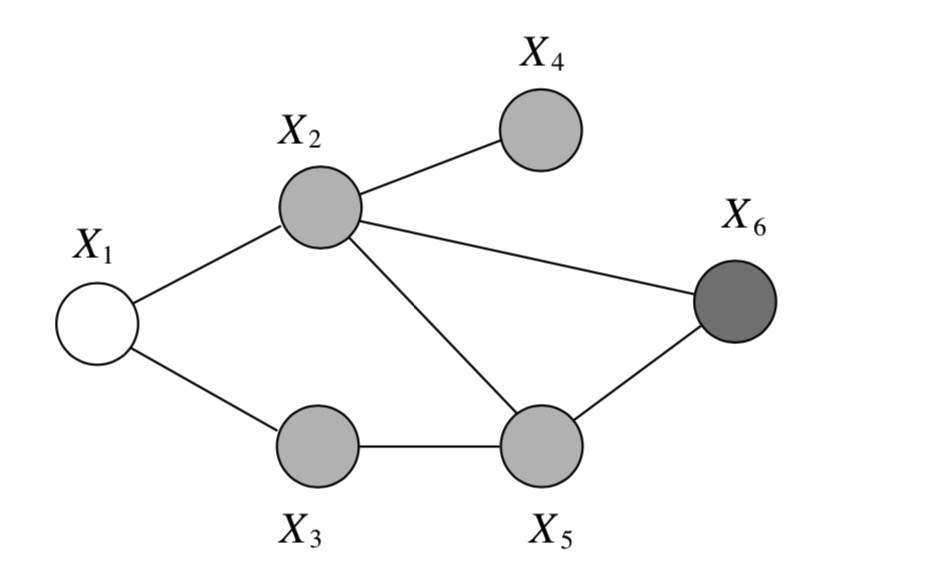
图 8.2.2 无向图示例，深色阴影结点 \(\mathrm{x}_6\) 是条件变量；浅色阴影结点， \(\{\mathrm{x}_2,\mathrm{x}_3,\mathrm{x}_4,\mathrm{x}_5\}\) ，是需要边际化消除的变量集合； \(\mathrm{x}_1\) 是查询结点。

如 图 8.2.2 ，我们继续以查询条件概率 \(p(x_1|\bar{x}_6)\) 为例，我们用定义在团上的势函数表示这个无向图的联合概率分布， 图上的团有 \(\{\mathrm{x_1},\mathrm{x_2}\},\{\mathrm{x_1},\mathrm{x_3}\},\{\mathrm{x_2},\mathrm{x_4}\},\{\mathrm{x_3},\mathrm{x_5}\},\{\mathrm{x_2},\mathrm{x_5},\mathrm{x_6}\}\) ，则这个无向图的联合概率分布为：

(8.2.51)\[p_{\mathbf{x}}(\mathbf{x}) =\frac{1}{Z} \varphi_{12}(x_1,x_2) \varphi_{13}(x_1,x_3) \varphi_{24}(x_2,x_4) \varphi_{35}(x_3,x_5) \varphi_{256}(x_2,x_5,x_6)\]

类似于有向图的推断过程，首先我们计算未归一化的条件概率 \(p(x_1,\bar{x}_6)\) 。

(8.2.52)\[ \begin{align}\begin{aligned}p(x_1,\bar{x}_6) &= \frac{1}{Z} \sum_{x_2}\sum_{x_3}\sum_{x_4}\sum_{x_5}\sum_{x_6} \varphi_{12}(x_1,x_2) \varphi_{13}(x_1,x_3) \varphi_{24}(x_2,x_4) \varphi_{35}(x_3,x_5) \varphi_{256}(x_2,x_5,x_6) \delta(x_6,\bar{x}_6)\\&= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2)\sum_{x_3} \varphi_{13}(x_1,x_3) \sum_{x_4} \varphi_{24}(x_2,x_4) \sum_{x_5} \varphi_{35}(x_3,x_5) \sum_{x_6} \varphi_{256}(x_2,x_5,x_6) \delta(x_6,\bar{x}_6)\\&= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2)\sum_{x_3} \varphi_{13}(x_1,x_3) \sum_{x_4} \varphi_{24}(x_2,x_4) \sum_{x_5} \varphi_{35}(x_3,x_5) m_6(x_2,x_5)\\ &= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2)\sum_{x_3} \varphi_{13}(x_1,x_3) m_5(x_2,x_3) \sum_{x_4} \varphi_{24}(x_2,x_4)\\&= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2) m_4(x_2) \sum_{x_3} \varphi_{13}(x_1,x_3) m_5(x_2,x_3)\\ &= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2) m_4(x_2) m_3(x_1,x_2)\\ &= \frac{1}{Z} m_2(x_1)\end{aligned}\end{align} \]

对 \(x_1\) 进行求和边际化可得到归一化因子：

(8.2.53)\[p(\bar{x}_6) = \frac{1}{Z} \sum_{x_1} m2(x_1)\]

然后我们就能得到想要查询的条件概率 \(p(x_1|\bar{x}_6)\) ：

(8.2.54)\[p(x_1|\bar{x}_6) = \frac{m_2(x_1)}{\sum_{x_1} m_2(x_1)}\]

我们发现无向图的归一化系数Z无需计算出来，在进行条件概率查询时可以消除掉。 然而当我们需要计算边缘概率 \(p(x_i)\) 时，这个系数Z就无法被消除了，需要被准确的计算出来。 但也不是很困难，系数Z其实就是对联合概率分布中全部变量进行求和消除的结果 ， 我们在求边缘概率 \(p(x_i)\) 时，已经在执行变量消除了， 消除了除变量 \(x_i\) 以外的所有结点得到 \(m_i(x_i)\) ， 这时有 \(Z=\sum_{x_i} m_i(x_i)\) 。 具体举例说明下，还是这个无向图，假设想要查询边缘概率 \(p(x_1)\) ，不是条件概率，没有证据变量，也就不需要引入 \(\delta(\cdot)\)

(8.2.55)\[ \begin{align}\begin{aligned}p(x_1) &= \frac{1}{Z} \sum_{x_2}\sum_{x_3}\sum_{x_4}\sum_{x_5}\sum_{x_6} \varphi_{12}(x_1,x_2) \varphi_{13}(x_1,x_3) \varphi_{24}(x_2,x_4) \varphi_{35}(x_3,x_5) \varphi_{256}(x_2,x_5,x_6)\\&= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2)\sum_{x_3} \varphi_{13}(x_1,x_3) \sum_{x_4} \varphi_{24}(x_2,x_4) \sum_{x_5} \varphi_{35}(x_3,x_5) \sum_{x_6} \varphi_{256}(x_2,x_5,x_6)\\&= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2)\sum_{x_3} \varphi_{13}(x_1,x_3) \sum_{x_4} \varphi_{24}(x_2,x_4) \sum_{x_5} \varphi_{35}(x_3,x_5) m_6(x_2,x_5)\\ &= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2)\sum_{x_3} \varphi_{13}(x_1,x_3) m_5(x_2,x_3) \sum_{x_4} \varphi_{24}(x_2,x_4)\\&= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2) m_4(x_2) \sum_{x_3} \varphi_{13}(x_1,x_3) m_5(x_2,x_3)\\ &= \frac{1}{Z} \sum_{x_2} \varphi_{12}(x_1,x_2) m_4(x_2) m_3(x_1,x_2)\\&= \frac{1}{Z} m_2(x_1)\end{aligned}\end{align} \]

这时有：

(8.2.56)\[Z= \sum_{x_1} \sum_{x_2}\sum_{x_3}\sum_{x_4}\sum_{x_5}\sum_{x_6} \varphi_{12}(x_1,x_2) \varphi_{13}(x_1,x_3) \varphi_{24}(x_2,x_4) \varphi_{35}(x_3,x_5) \varphi_{256}(x_2,x_5,x_6) =\sum_{x_1} m_2(x_1)\]

无向图的消元算法和有向图本质上是一样的，消元法的本质就是找到一个合适顺序进行边际化消除变量。

8.3. 图消除

待处理

待补充

8.4. 总结

• 概率图推断通常关注两个问题: a.边缘概率查询；b.条件概率查询，有时也称为后验概率。

• 消元法的本质就是找到一个合适的顺序进行变量的边际化(离散变量求和，连续变量积分)。

• 消元法的相比原始方法提高了计算效率。