1. 贝叶斯知识追踪(Bayesian Knowledge Tracing,BKT)

1.1. 简介

目前在教育领域的数据挖掘应用中，很重要的一个场景就是对学生的学习过程进行建模。 当前行业内比较流行的一种建模方式就是贝叶斯知识追踪(Bayesian Knowledge Tracing,BKT)， 由Corbett, A. T. 和 Anderson, J. R.在1995年提出 [1] 。直到今日，仍然有很多人在研究改进BKT模型。

虽然BKT模型在很多场景下效果良好，但还是存在一些不足的。其中一个不足之处就是，BKT是对”知识点”进行建模的，没有包含”学生个体”和”题目”的差异信息。 本文讨论的是一种通过结合IRT（项目反应理论，Item Response Theory）模型进而引入题目信息的方法。

1.2. 隐马尔科夫模型(Hidden Markov Model,HMM)

BKT模型其实质就是一个标准的HMM模型，所以在学习BKT之前，需要先学习了解HMM模型。 本文暂且不做详细说明，请读者查阅其它相关资料（ [2] , [3] , HMM学习最佳范例 ）。

1.3. 贝叶斯知识追踪(Bayesian Knowledge Tracing)

通常场景下，学生对一个知识点的学习是一个过程，学习过程中往往伴随着作答练习题辅助学习。 学生对知识点的学习结果(掌握状态)影响着题目的作答结果，并且整个过程中学生对于知识点的掌握状态也在发生变化，从未掌握到掌握的变化。 整个过程非常符合HMM的建模过程。

贝叶斯知识追踪模型，就是利用HMM模型对学生知识点下题目作答进行建模的方法，学习过程，就是HMM的序列过程。

• 初始情况下，学生对当前知识点的状态（掌握、未掌握）概率，作为HMM的初始概率变量。

• 学习过程中，学生是否掌握当前知识点的状态（掌握、未掌握）作为HMM的隐状态。

• 学习过程中，知识点掌握状态在发生变化，也即是HMM的状态转移。

• 学习过程中，学生对当前知识点下题目的作答结果(做对、做错)作为HMM的观测变量。

• 学习过程中，学生会不停的作答练习题，题目的作答结果序列就作为HMM的观测序列。

我们用0代表学生”未掌握”当前知识点，用1代表”掌握”了知识点；用0代表学生作答题目错误，1代表学生作答题目正确。 隐状态集合为：

(1.3.11)\[S=\{0(未掌握),1(掌握)\}\]

观测变量集合为:

(1.3.12)\[V=\{0(作答错误),1(作答正确)\}\]

初始状态下，学生对当前知识点的”掌握”的概率为 \(P(L_0)\) ,则”未掌握”的概率是 \(1-P(L_0)\) ，HMM的初始概率矩阵为:

(1.3.13)\[\pi = [1-P(L_0),P(L_0)]\]

学习过程中，学生知识点掌握状态发生变化。假设从”未掌握”到”掌握”的学习进步概率为 \(P(T)\) ,HMM的转移概率矩阵为：

(1.3.14)\[\begin{split}A = \left [ \begin{matrix} & 未掌握 & 掌握 \\ 未掌握 & 1-P(T) & P(T) \\ 掌握 & 0 & 1 \end{matrix} \right ]\end{split}\]

备注

这里我们假设状态为”掌握”时，将不再发生变化。也就是状态不会从”掌握”到”未掌握”转变。

学生对题目的作答正确与否，会受到隐状态(知识点的掌握情况)的影响，不同隐状态作答题目正确概率不同，形成HMM的观测(发射)概率矩阵。 理想情况下，当隐状态是”未掌握”时，学生应该做错题目；当隐状态是”掌握”时，学生应该做对题目。 但实际中，即使学生”未掌握”知识点也有一定可能猜对题目，我们假设猜测(Guess)的概率为 \(P(G)\) ; 即使学生”掌握”了知识点，也可能做错题目，我们假设失误(Slip)的概率为 \(P(S)\) 。

(1.3.15)\[\begin{split} B = \left [ \begin{matrix} & 错误 & 正确 \\ 未掌握 & 1-P(G) & P(G) \\ 掌握 & P(S) & 1-P(S) \end{matrix} \right ]\end{split}\]

学生在学习过程中，题目的作答结果序列就是HMM的观测序列。

(1.3.16)\[O=[0,1,1,0,1,0,...]\]

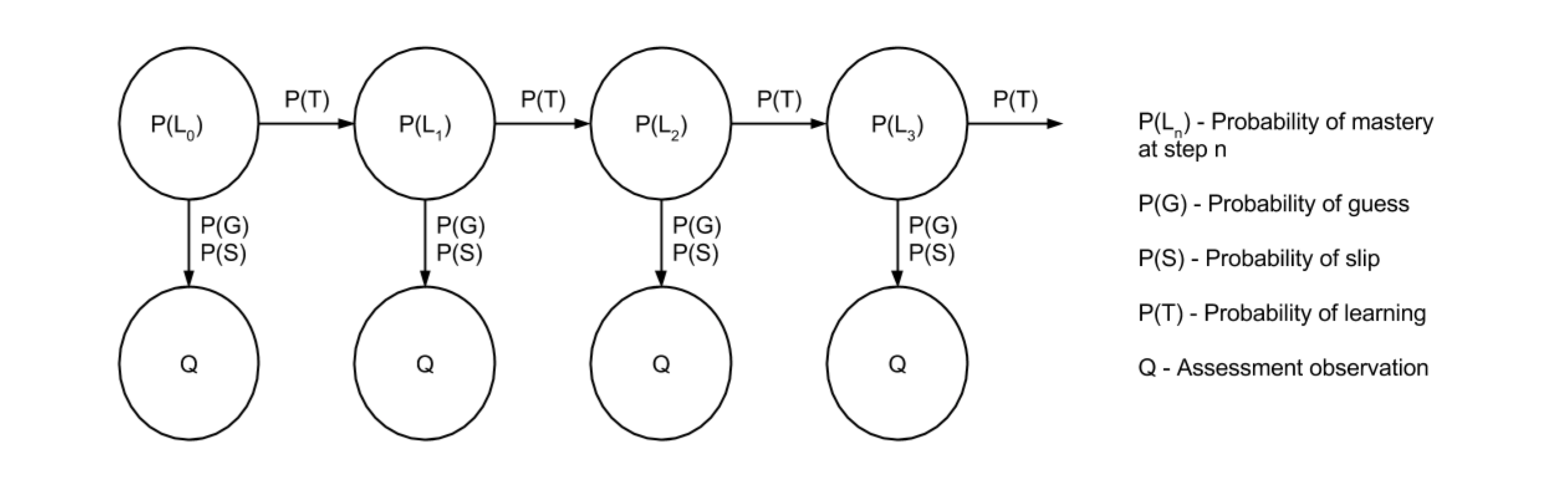
BKT模型是对”知识点”的建模，也就是一个”知识点”训练一个BKT模型，同一个”知识点”下多个学生的作答序列，作为多个独立的观测序列进行模型训练。

BKT模型的应用 ===========================================NeuralNetwork.rst

通过历史学生作答数据，训练知识点的BKT模型，得到一个知识点的BKT模型。已知一个知识点的BKT模型后，一般有两种应用。

1. 判断一个学生对当前知识点的”掌握”状态。已知BKT(HMM)模型，解码隐状态序列。

2. 预测一个学生题目作答结果。已知BKT(HMM)模型和观测序列（学生的作答序列），预测下一个观测值(下一题作答结果)。

1.3.1. BKT的参数估计

BKT模型实际就是一个标准的HMM模型，其参数估计过程就是HMM模型的参数估计过程，具体参数估计算法可以参考以下资料：

• 李航的《统计学习》

• Christopher M Bishop: Pattern Recognition and Machine Learning

• Dawei Shen: Some Mathematics for HMM

重要

注意多观测序列和浮点数溢出问题。

1.4. 项目反映理论(Item Response Theory,IRT)

1.5. BKT结合IRT

标准BKT的缺点

BKT还是有很多缺点的，这里列举一些和本文相关的缺陷。

1. BKT是对知识点建模，没有做到学生的个性化。

2. BKT没有考虑题目的差异，事实上不同题目其难易程度等是不同的。

3. BKT的隐状态（知识掌握状态）只有”掌握”、”未掌握”两种状态，缺乏更丰富细致的表达。

BKT个性化不足的问题，其实比较容易解决，每个(知识点，学生)独立训练BKT模型即可。 但这样做也有很大不足，训练数据（作答序列）稀少，训练的模型效果很难保障。是否实用在具体的应用场景下去试验一下即可。

我们知道BKT模型是一个离散HMM模型，隐状态到观测值是通过一个概率矩阵表示。 我们可以用IRT模型替换这个观测矩阵，IRT的计算结果表示的是题目作答正确的概率，可以无缝对接。

IRT中学生的潜在能力状态 \(\theta\) 可以看成是学生对当前知识点的掌握情况， 这样就把BKT的隐状态的含义扩展成IRT中学生的潜在能力状态。 原始BKT中隐状态是一个二值变量，现在可以扩展成多个值(为了计算简单，这里仍然使用离散值)。 其值表示IRT中的 \(\theta\) ，IRT中的题目参数通过其他方法计算得到。

通过引入IRT，有两点改进

1. 可以引入题目差异信息。

2. 学生对知识点的掌握状态(隐状态)更加丰富。原来二值(“掌握”，”未掌握”)，扩展成多个值，更加有梯度。

不足的地方：

1. 没有找到同时估计题目参数的方法，需要提前用其他方法给出题目的参数信息。

为了简化，我们只采用单参数IRT模型(Rasch模型)

(1.5.5)\[P = \frac{1}{1+e^{-(\theta-b)}}\]

其中，\(\theta\) 表示HMM中的隐状态。 参数b表示题目难度。

隐状态的取值

为了计算简便，隐状态的取值为 [0,n]，n为隐状态的数量，每个值代表学生对知识点的掌握程度。0表示完全不会，n表示熟练掌握。

题目难度的计算

利用题目的正确率去表示题目难度，正确率越高题目难度越小；反之，正确率越低题目难度越大；

由于很多题目作答次数较少，正确率不能准确反映题目难度，我们采用 拉普拉斯修正 的方法计算题目正确率。

(1.5.6)\[ \begin{align}\begin{aligned}correct\_rate &= \frac{(correct\_count + 1)} { (correct\_count+wrong\_count + 2)}\\difficulty &= (1 - correct\_rate) * (stat\_count - \delta)\end{aligned}\end{align} \]

其中， \(\delta\) 是一个修正参数，由于IRT的特性，当 \(\theta=b\) 时，IRT的概率结果是 0.5， 而我们的模型中隐状态的最大值表示学生掌握知识点的极限值， 这时理论上学生能极大概率作答正确难度最高的题目，所以b的最大值要小于 \(\theta=b\) 的最大值，通过 \(\delta\) 调整二者之间的差值。

初始概率矩阵

(1.5.7)\[\pi = [p_0,p_1,...,p_n]\]

转移概率矩阵

(1.5.8)\[\begin{split}A = \left [ \begin{matrix} p_{00} & p_{01} & P_{0..} & p_{0n} \\ p_{..0} & p_{..1} & P_{...} & p_{..n} \\ p_{n0} & p_{n1} & P_{n..} & p_{nn} \\ \end{matrix} \right ]\end{split}\]

观测概率矩阵

(1.5.9)\[\begin{split} B = \left [ \begin{matrix} & 错误 & 正确 \\ 状态0 & 1-P(IRT|\theta=0) & P(IRT|\theta=0) \\ 状态1 & 1-P(IRT|\theta=1) & P(IRT|\theta=1) \\ .. & .. & .. \\ 状态n & 1-P(IRT|\theta=n) & P(IRT|\theta=n) \end{matrix} \right ]\end{split}\]

1.6. 实验

1.6.1. 数据集

我们使用 KDD Cup 2010 Educational Datamining Challenge (http://pslcdatashop.web.cmu.edu/KDDCup) 的公开数据集。

数据集是由 Carnegie Learning Inc 提供的，是学生在线上学习系统中的题目作答数据，数学课程中关于线性代数的学习数据。 我们这里使用 Development Data Sets ，包括三组数据，每组数据又分别包括train和test数据集。

表 1.6.1 Development Data Sets

Data sets	Students	Steps	Train Size	Test Size
Algebra I 2005-2006	575	813,661	809695	3968
Algebra I 2006-2007	1,840	2,289,726	2270384	19342
Bridge to Algebra 2006-2007	1,146	3,656,871	3679199	7672

表 1.6.2 Challenge Data Sets

Data sets	Students	Steps	Train Size	Test Size
algebra_2008_2009	3,310		8,918,055	508,913
bridge_to_algebra_2008_2009	6,043		20,012,499	756,387

详细的数据说明请参考 http://pslcdatashop.web.cmu.edu/KDDCup/rules_data_format.jsp

1.6.2. 实验方法

我们对比三种不同模型分别在上述三个数据集下的差异。

1. 原始BKT模型，每个知识点训练一个模型，别名：Standard-BKT。

2. 原始BKT模型，每个(知识点，学生)训练一个模型，别名：Individual-Standard-BKT。

3. IRT改进BKT模型，每个(知识点，学生)训练一个模型，别名：IRT-BKT 。

如何训练？

“Problem Hierarchy” 作为”知识点”，也就是每一个”Problem Hierarchy” 训练一个模型。 “Problem Name” + “Step Name” 作为题目的唯一标识。

小技巧

为什么不用 KC(KC Model Name) 列作为”知识点”？

首先BKT并不是必须对”知识点”进行建模，BKT本质是HMM，是对一个学习过程建模，所以一个独立的学习单元(“Problem Hierarchy”)同样可以建模。 KDD cup 的数据集中，每个题目的KC(KC Model Name)列包含多个知识点，非常难于处理（实际效果也不好）， 所以这里我们选择”Problem Hierarchy”作为”知识点”。

测试集中的数据无法全部预测

对于test测试集中的每条数据，不一定都能训练得到对应的模型。比如

1. 对于 Individual-Standard-BKT 模型，可能当前(知识点，学生)在训练集只有一条作答数据，无法训练模型，也就无法预测。

2. 对于 IRT-BKT 模型，可能test中的某个题目，在训练集中未出现过，无法得到题目难度参数，也将无法预测。

总之，是无法保证测试集中所有数据都能使用训练好的模型进行预测，这样的数据我们就抛弃，既然无法预测也就不能反映模型预测效果。

1.6.3. 实验结果

1.6.3.1. 开发数据集(Development Data Sets)

test size:

可以成功预测的测试集数据量

correct rate:

测试集中学生作答结果正确率

rmse:

Root Mean Squared Error (RMSE)，均方根误差。

acc:

模型预测的准确率

delta_acc:

acc 和 correct rate 的差值

表 1.6.3 对比报告

data	model	test size	correct rate	rmse	auc_score	acc	delta_acc
bridge_to_algebra_2006_2007	IRT-BKT	7069	0.8495	0.3169	0.8121	0.8741	0.0246
bridge_to_algebra_2006_2007	Individual-Standard-BKT	7437	0.8478	0.3418	0.7375	0.8505	0.0027
bridge_to_algebra_2006_2007	Standard-BKT	7607	0.8436	0.3471	0.7075	0.8488	0.0053
bridge_to_algebra_2006_2007	IRT	7294	0.8427	0.3190	0.8202	0.8658	0.0230
algebra_2005_2006	IRT-BKT	3134	0.7849	0.3713	0.7804	0.8191	0.0341
algebra_2005_2006	Individual-Standard-BKT	3774	0.7909	0.4003	0.6350	0.7925	0.0016
algebra_2005_2006	Standard-BKT	3910	0.7900	0.4019	0.6051	0.7908	0.0008
algebra_2005_2006	IRT	3276	0.7817	0.3617	0.7934	0.8288	0.0470
algebra_2006_2007	IRT-BKT	7032	0.7683	0.3739	0.7993	0.8185	0.0502
algebra_2006_2007	Individual-Standard-BKT	9408	0.7828	0.4002	0.6716	0.7868	0.0039
algebra_2006_2007	Standard-BKT	9678	0.7815	0.4030	0.6387	0.7859	0.0044
algebra_2006_2007	IRT	14729	0.7844	0.3622	0.7870	0.8231	0.0387
智能练习数据	IRT-BKT	3988	0.6311	0.4787	0.7510	0.6863	0.0552
智能练习数据	Individual-Standard-BKT	4015	0.6311	0.4882	0.6174	0.6508	0.0197
智能练习数据	Standard-BKT	4015	0.6311	0.4829	0.5787	0.6421	0.0110
智能练习数据	IRT	3988	0.6311	0.4399	0.7535	0.7119	0.0807

结论:

预测学生作答结果的正确率上有3%的提升，

均方根误差(rmse)有2%~8%的提升。

1.6.3.2. 挑战数据集(Challenge Data Sets)

KDD CUP 2010 Challenge 榜单结果

我们的模型得分:

Cup Scoring	Leaderboard Scoring
0.3090	0.3165

图 1.6.1 cup score of team acmtiger

1.6.4. 项目代码

为了性能，BKT算法采用c++编写，利用 cython 实现python api。

BKT项目代码

本文实验入口文件

1.7. 未来工作

1.7.1. 题目难度的计算

1.7.2. 多参数IRT模型

1.7.3. 参数估计算法

目前使用的期望最大化算法(EM,expectation maximization method)参数估计算法， 后续可以尝试使用 Conjugate Gradient Search [1], or discretized brute-force search [7]

摘自 Individualized Bayesian Knowledge Tracing Models

Instead of a traditional Expectation Maximization (EM) method
for learning BKT parameters,
we base our method on the so-called optimization techniques
approach described in [2] for the following reasons.

First, EM does not directly optimize a likelihood of the
student observations given BKT parameters
(a standard metric for HMM).
As a result, the EM algorithm could make adjustments to
BKT parameters that would actually worsen the fit.

Second, using the gradient- based optimization techniques
allows us to introduce student-specific parameters to BKT
without expanding the structure of the underlying HMM (cf. [5]).
Keeping the structure of the underlying HMM unchanged
permits us to lower the computational cost of fitting

1.8. 参考文献

[1]

Corbett, A. T. and Anderson, J. R.: Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction, 4(4), 253-278. (1995)

[2]

李航 : 统计学习方法

[3]

Christopher M Bishop : Pattern Recognition and Machine Learning

[4]

Dawei Shen : Some Mathematics for HMM

[5]

Radek Pel´anek : Bayesian Knowledge Tracing, Logistic Models, and Beyond: An Overview of Learner Modeling Techniques

[6]

Michael V. Yudelson, Kenneth R. Koedinger, and Geoffrey J. Gordon : Individualized Bayesian Knowledge Tracing Models