11. 完整观测的参数学习

我们已经讲述了概率图模型的表示以及基于图结构的模型推断算法， 概率图模型有三种图形，分别是有向图、无向图和因子图，每种图形都有自己的特色。 其中有向图表达的是变量之间的单向关系，而无向图则可以表达变量之间的相互关系， 因子图直接表达联合概率的因子分解。 一个概率图模型表达的联合概率分布， 我们可以利用模型推断算法推断出这个联合概率中的边缘概率或者条件概率。 在模型推断过程中，都是建立在模型已知的前提下，模型结构是已知的，模型的联合概率分布的表达式是已知的。 对于有向图，联合概率中的每个局部条件概率表达式都是确定性的； 对于无向图和因子图，联合概率中的每个势函数都是确定性的。

然而，有些时候对于一个概率图模型可能存在一些未知的量，可能是模型结构未知， 可能是模型的联合概率表达式中存在未知参数，亦或者两者都未知。 幸运的是，如果我们能获取到模型的观测样本，我们可以利用这些观测数据学习出模型的未知量。 图模型的学习一般包含模型结构(graphical structure)的学习 和模型参数(parameters or potentials)的学习。训练数据可以是全部变量(图中结点)的观测值， 也可以仅是部分变量(结点)观测数据。如果训练数据仅包含图中部分变量的观测值，我们称之为”不完整观测”， 没有观测到的变量称为”隐变量(latent variables)” 。 鉴于此，图模型的学习问题通常有如下4类场景。

1. 模型结构已知，模型参数未知，拥有 完整 的观测数据去学习模型参数。

2. 模型结构已知，模型参数未知，拥有 不完整 的观测数据去学习模型参数。

3. 模型结构和模型参数均未知，拥有 完整 的观测数据去学习结构和参数。

4. 模型结构和模型参数均未知，拥有 不完整 的观测数据去学习模型参数。

在后续的章节中，我们会分别讨论上述场景中模型学习问题，本章我们讨论第一个场景，即拥有完整观测数据的情况下，学习模型的参数。 在 章节2参数估计 中我们讲述了单变量概率分布的参数估计算法， 同样是利用观测样本进行参数估计，有最大似然估计和贝叶斯估计两种参数估计算法。贝叶斯估计和最大似然估计有着很大的相似性， 贝叶斯估计可以看做是在最大似然估计的基础上加入了参数的先验。 多变量概率图模型的参数估计和单变量概率分布的参数估计，没有本质差别，同样可以使用最大似然和贝叶斯两种估计算法。 这是因为联合概率分布乘积形式可以分解成每个结点独立估计。

11.1. 有向图的参数学习

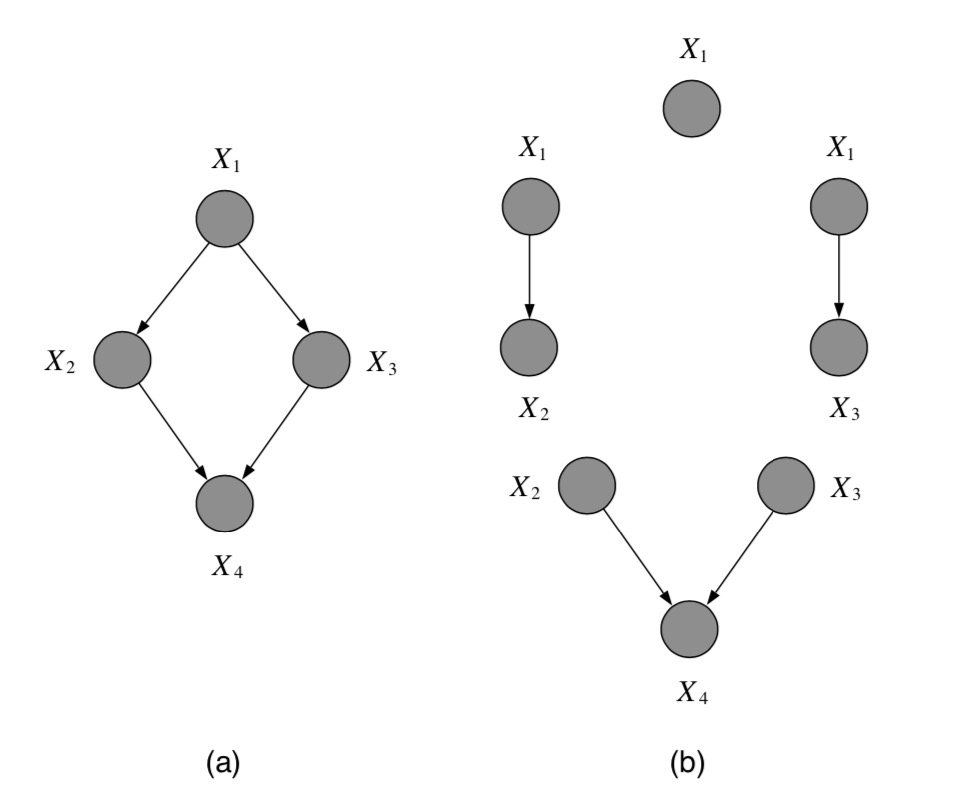
图 11.1.1 (a)一个有向图。(b)有向图(a)的最大似然问题等价于局部条件概率的独立最大似然问题。结点的灰色阴影表示这个结点是可观测的。

让我们从一个有向图模型的例子开始， 图 11.1.1 (a)是一个4结点的有向图模型， 这个图模型的联合概率分布为：

(11.1.3)\[p(x_1,\dots,x_4)=p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_4|x_2,x_3)\]

我们假设上述因子分解式中每个子项都包含有未知参数， 则这个联合概率分布含有4个 参数向量 \(\pmb{\theta}_1,\pmb{\theta}_2,\pmb{\theta}_3,\pmb{\theta}_4\) ， 每个 \(\pmb{\theta}_i\) (粗体)是个参数集合， 每个结点 \(X_i\) 与其父结点的条件概率分布是由 \(\pmb{\theta}_i\) 定义的。 参数化后的联合概率为：

(11.1.4)\[p(x_1,\dots,x_4;\pmb{\theta}_1,\pmb{\theta}_2,\pmb{\theta}_3,\pmb{\theta}_4)=p(x_1;\pmb{\theta}_1) p(x_2|x_1;\pmb{\theta}_2)p(x_3|x_1;\pmb{\theta}_3) p(x_4|x_2,x_3;\pmb{\theta}_4)\]

假设观测到模型的一些样本，图中每个变量都能观测到，每条样本都包含4个随机变量的观测值，用符号 \(\mathcal{D}\) 表示观测样本集，样本集的规模是N。 则这个观测样本的对数似然函数可以写成：

(11.1.5)\[ \begin{align}\begin{aligned}\ell(\mathbf{x};\pmb{\theta}) &= log \prod_{i=1}^N p(x_1,x_2,x_3,x_4;\pmb{\theta}_1,\pmb{\theta}_2,\pmb{\theta}_3,\pmb{\theta}_4)^{(i)}\\&= log \prod_{i=1}^N [ p(x_1;\pmb{\theta}_1)p(x_2|x_1;\pmb{\theta}_2)p(x_3|x_1;\pmb{\theta}_3)p(x_4|x_2,x_3;\pmb{\theta}_4)]^{(i)}\\ &= \sum^{N}_{i=1} \left [ log p(x_1;\pmb{\theta}_1) + log p(x_2|x_1;\pmb{\theta}_2) + log p(x_3|x_1;\pmb{\theta}_3) + log p(x_4|x_2,x_3;\pmb{\theta}_4) \right ]^{(i)}\\&= \sum^{N}_{i=1} log p(x_1;\pmb{\theta}_1)^{(i)} + \sum^{N}_{i=1} log p(x_2|x_1;\pmb{\theta}_2)^{(i)} + \sum^{N}_{i=1} log p(x_3|x_1;\pmb{\theta}_3)^{(i)} + \sum^{N}_{i=1} log p(x_4|x_2,x_3;\pmb{\theta}_4)^{(i)}\end{aligned}\end{align} \]

可以看到，上述公式是4个子项 相加 ，而每个参数集 \(\pmb{\theta}_i\) 都只出现在其中一项中， 所以在极大化优化中，可以分别独立进行的最优化（每个子项分别取得极大值时，整体也是极大值）。 如图 图 11.1.1 (b)所示，有向图联合概率的最大似然估计可以分解成各个局部条件概率的局部最大似然估计。

举个例子，假设这个有向图模型中的变量都是离散变量，对于结点变量 \(X_3\) ， 假设其取值空间为 \(a_{31},a_{32},a_{33}\) 共有三个取值， 也就是说变量 \(X_3\) 是一个三值离散变量。其父结点变量 \(X_1\) 取值空间是 \(a_{11},a_{12}\) 共两个取值，是一个二值离散变量。 其中 \(\pmb{\theta}_3=[\theta_{31},\theta_{32},\theta_{33},\theta_{34},\theta_{35},\theta_{36}]\) ，\(\theta_{31}\) 表示 \(p(\mathrm{x}_3=a_{31}|\mathrm{x}_1=a_{11})=\theta_{31}\) ，其他参数值类似， 并且满足约束 \(\theta_{31} + \theta_{32} + \theta_{33}=1,\theta_{34} + \theta_{35} + \theta_{36}=1\) 。 条件概率分布 \(p(x_3|x_1;\pmb{\theta}_3)\) 用表格形式表示如下：

(11.1.6)\[\begin{split}\begin{array}{|c|c|c|c|} \hline & x_3=a_{31} &x_3=a_{32} &x_3=a_{33} \\\hline x_{1}=a_{11}& \theta_{31} &\theta_{32} &\theta_{33} \\\hline x_{1}=a_{12}& \theta_{34} &\theta_{35} &\theta_{36} \\\hline \end{array}\end{split}\]

此外，条件概率 \(p(x_3|x_1;\pmb{\theta}_3)\) 可以表示成：

(11.1.7)\[p(x_3|x_1;\pmb{\theta}_3) = p(x_3|x_1=a_{11};\theta_{31} ,\theta_{32} ,\theta_{33})+ p(x_3|x_1=a_{12};\theta_{34} ,\theta_{35} ,\theta_{36})\]

在求解偏导数前先定义一些统计量，我们用 \(D(x_1=a_{11})\) 表示在样本集D中变量 \(x_1\) 取值为 \(a_{11}\) 的样本子集， \(N(x_1=a_{11})\) 表示样本子集 \(D(x_1=a_{11})\) 的数量； 同理 \(D(x_1=a_{12})\) 表示在样本集D中变量 \(x_1\) 取值为 \(a_{12}\) 的样本子集， \(N(x_1=a_{12})\) 表示样本子集 \(D(x_1=a_{12})\) 的数量。 极大化对数似然函数 \(\ell(\mathbf{x};\pmb{\theta})\) 对参数 \(\pmb{\theta}_3\) 的偏导数为：

(11.1.8)\[ \begin{align}\begin{aligned}\frac{\partial \ell }{\partial \pmb{\theta_3} } &=\frac{\partial }{\partial \pmb{\theta_3} } \sum^{N}_{i=1} log p(x_3|x_1;\pmb{\theta}_3)^{(i)}\\&= \frac{\partial }{\partial \pmb{\theta_3} } \left [ \sum_{i \in D(x_1=a_{11})} p(x_3|x_1=a_{11};\theta_{31} ,\theta_{32} ,\theta_{33})^{(i)} + \sum_{j \in D(x_1=a_{12})} p(x_3|x_1=a_{12};\theta_{34} ,\theta_{35} ,\theta_{36})^{(j)} \right ]\\ &= \frac{\partial }{\partial \pmb{\theta} } \sum_{i \in D(x_1=a_{11})} p(x_3|x_1=a_{11};\theta_{31} ,\theta_{32} ,\theta_{33})^{(i)} + \frac{\partial }{\partial \pmb{\theta} } \sum_{j \in D(x_1=a_{12})} p(x_3|x_1=a_{12};\theta_{34} ,\theta_{35} ,\theta_{36})^{(j)}\end{aligned}\end{align} \]

\(p(x_3|x_1=a_{11};\theta_{31} ,\theta_{32} ,\theta_{33})\) 与 \(p(x_3|x_1=a_{12};\theta_{34} ,\theta_{35} ,\theta_{36})\) 分别是一个多项式分布(或者类别分布)，并且是可以分开独立进行极大似然估计的，前者估计的的样本集为 \(D(x_1=a_{11})\) ， 而后者的样本集为 \(D(x_1=a_{12})\) 。 根据极大似然估计的充分统计量，可以得出：

(11.1.9)\[ \begin{align}\begin{aligned}(\hat{\theta}_{31})_{ML} = \frac{N(x_1=a_{11},x_3=a_{31})}{N(x_1=a_{11})}\\(\hat{\theta}_{32})_{ML} = \frac{N(x_1=a_{11},x_3=a_{32})}{N(x_1=a_{11})}\\(\hat{\theta}_{33})_{ML} = \frac{N(x_1=a_{11},x_3=a_{33})}{N(x_1=a_{11})}\\ (\hat{\theta}_{34})_{ML} = \frac{N(x_1=a_{12},x_3=a_{34})}{N(x_1=a_{12})}\\(\hat{\theta}_{35})_{ML} = \frac{N(x_1=a_{12},x_3=a_{35})}{N(x_1=a_{12})}\\(\hat{\theta}_{36})_{ML} = \frac{N(x_1=a_{12},x_3=a_{36})}{N(x_1=a_{12})}\end{aligned}\end{align} \]

有向图的最大似然估计与单个变量的最大似然估计是一样的。 无非就是单一变量的概率分布 \(p(\mathrm{x}|\theta)\) ，变成了多变量的联合概率分布 \(p(\mathrm{x}_1,\ldots,\mathrm{x}_N|\theta)\) 。

对比项	单变量	有向图
概率分布	\(p(\mathrm{x}|\theta)\)	\(p(\mathrm{x}_1,\ldots,\mathrm{x}_N |\theta)=\prod_k p(\mathrm{x}_k | pa_k,\theta)\)
似然函数	\(\prod_{s} p(\mathrm{x}^s|\theta)\)	\(\prod_s \prod_k p(\mathrm{x}_k | pa_k,\theta)\)
对数似然函数	\(\sum_s log p(\mathrm{x}^s|\theta)\)	\(\sum_s \sum_k log p(\mathrm{x}_k | pa_k,\theta)\)

有向图的联合概率分布是可以分解成多个因子的乘积的，对数似然函数又可以把乘法转变成加法，只要各个参数是独立的， 加法的各项在极大化求解的过程中是可以独立进行的。同理有向图的贝叶斯估计也是类似的，无非就是在似然估计的基础上增加了先验分布。

重要

值得强调的最大似然问题可以分解成独立的子问题依赖两个条件。 首先，我们有完整的观察数据集，即所有的观察元组样本都给出了所有变量的值。 其次，对于每个条件概率分布(CPD)，参数是相互独立的。 如果这两个条件有任意一个不满足，则最大似然问题不会分解为每个变量上的独立子问题。

11.2. 无向图的参数学习

有向图的联合概率中因子函数被限定为结点及其父结点上的局部条件概率，但是在无向图中， 联合概率的因子函数是未归一化的势函数，所以无向图的联合概率表达式需要一个全局归一化系数Z。 这个归一化系数把所有参数都耦合在一起，使得无法把局部参数分解独立估计，令无向图的参数估计变得十分复杂。 然而，有一类特殊的无向图结构是可以进行参数解耦的，并且可以独立的估计局部参数。

一般形式的无向图参数估计方法是很复杂的，本节所介绍的无向图参数估计方法是在特定的限制条件下才有效的方法，需要满足如下条件：

• 无向图中的随机变量是离散变量。

• 图中定义在每个团C上的团势函数的形式为 \(\theta_C \prod_{k\in C } x_k\) ，其中 \(\theta_C\) 为这个团上的参数。

• 观测样本集足够多，无向图联合分布的所有可能取值都有足够多的观测样本。比如，无向图结点（随机变量）数量是N，每个随机变量的取值空间 \(|\mathcal{X}|=M\) ，则所有变量的可能取值规模是 \(N^M\) ，观测样本要覆盖到每一种取值。

我们令 \(\mathcal{G}=(V,E)\) 表示一个无向图模型，其中 \(V=\{1,\dots,N \}\) 表示N个结点集合， \(E \subseteq V \times V\) 表示图中的无向边集合。 相关联的随机变量为离散空间 \(\mathcal{X}\) 中的变量集 \(\mathrm{x}_1,\dots,\mathrm{x}_N\) 。 为简单，在本节中，我们约定 \(\mathcal{X} \in \{0,1\}\) ，但是本节中介绍的算法同时适用于任意大小的 \(\mathcal{X}\) 空间， 同时要满足 \(p(\mathbf{x} >0),\forall \mathbf{x} \in \mathcal{X}^N\) 。 回想一下无向图的因子分解表达(Hammersley-Clifford 定理)，无向图的联合概率分布可以表示为：

(11.2.1)\[p(\mathbf{x})=exp(\sum_{C \in \mathcal{e}(G)} V_C(\mathbf{x}_C) )\]

其中 \(\mathcal{e}(G)\) 是图G中所有团集合，包括空集（PS：我理解应该是单个结点组成的团）， \(\mathbf{x}_C=(x_i)_{i\in C}\) 表示属于团C中的所有结点变量， \(V_C\) 是定义在团C上的势函数(potential function)。

(11.2.2)\[\begin{split}V_C(\mathbf{x}_C) = \left\{ \begin{aligned} Q(C)& \ \ if \ \mathbf{x}_C =1 \\ 0& \ \ otherwise \\ \end{aligned} \right.\end{split}\]

我们从这个分布中观测到i.i.d. 的样本表示为 \(\mathcal{D}=\{\mathbf{x}^{(1)},\dots,\mathbf{x}^{(S)}\}\) 。 我们的任务是从观测数据集 \(\mathcal{D}\) 学习出图模型 \(G\) 中每个团上势函数。

11.2.1. 成对二值变量模型

我们先讨论一个简单的图模型，即图中每个团都只包含两个结点，以及单个结点上定义的因子。 \(\mathcal{e}(G)\) 包含所有的结点集V，边集合E，以及空集，同样，\(\mathcal{X} \in \{0,1\}\) 。 图中每条边定义一个独立的团，以及每个结点单独定义一个因子。给定这些条件，无向图模型的可以用下式表示：

(11.2.3)\[p(\mathbf{x})= \frac{1}{Z} exp(\sum_{i \in V} \theta_i x_i + \sum_{(i,j)\in E} \theta_{ij} x_i x_j)\]

其中 \(\theta_i x_i\) 是定义在单个结点上势函数， \(\theta_{ij} x_i x_j\) 是定义在每个二元团（每条边组成一个团，即团内只包含两个结点）上的势函数。 对于任意 \(\theta_i,\theta_{ij} \in \mathbb{R}, \forall i \in V, (i,j) \in E\) ，Z是归一化常量。 至此，这个问题归结起来就是从观测数据集 \(\mathcal{D}\) 中学习参数 \(\pmb{\theta}\) ，其中

(11.2.4)\[\pmb{\theta} = (\theta_i, i \in V; \theta_{ij} ,(i,j) \in E )\]

如果我们有一个很大规模的观测数据集( \(>>2^N\) )，保证每种 \(\mathbf{x}=\{\mathrm{x}_1,\ldots,\mathrm{x}_N\},\mathbf{x}\in \{0,1\}^N\) 可能取值都有足够的样本。 我们就可以根据经验概率(empirical probability)分布来估计参数值。

我们利用无向图的一个典型特点： 对于任意 \(i \in V\) ，给定 \(\mathrm{X}_{N(i)}\) ( \(N(i)\) 表示结点i的邻居结点集合)， \(X_i\) 与其他非邻居结点相互独立，即图中任意结点在给定其邻居结点的条件下独立于其它非邻居结点，结点i的非邻居结点用符号 \(X_{V \backslash (N(i) \cup \{i\})}\) 。 则有：

(11.2.5)\[p(\mathrm{x}_i=\cdot | \mathbf{x}_{N(i)} = \mathbf{0}) = p(\mathrm{x}_i=\cdot|\mathbf{x}_{V\backslash \{i\}} = \mathbf{0})\]

上式的意思是，等号左边是：结点变量i的邻居结点都为0的条件下结点变量 \(\mathrm{x}_i\) 的条件概率分布， 等号右边是：除结点i以外所有结点都为0的条件下结点变量 \(\mathrm{x}_i\) 的条件概率分布，而两者是等同的， 背后的理由就是无向图的条件独立属性。

另外 \(p(\mathrm{x}_i=1|\mathbf{x}_{N(i)} = \mathbf{0})\) 与 \(p(\mathrm{x}_i=0|\mathbf{x}_{N(i)} = \mathbf{0})\) 的比值是同一个条件概率分布的两种取值的比值，这个比值是可以去掉Z的。

(11.2.6)\[ \begin{align}\begin{aligned}& \ log \frac{p(\mathrm{x}_i=1|\mathbf{x}_{N(i)} = \mathbf{0})}{p(\mathrm{x}_i=0|\mathbf{x}_{N(i)} = \mathbf{0})}\\&= log \frac{p(\mathrm{x}_i=1|\mathbf{x}_{V\backslash \{i\}} = \mathbf{0})}{p(\mathrm{x}_i=0|\mathbf{x}_{V\backslash \{i\}} = \mathbf{0})}\\&= log \frac{exp(\sum_{i\in V} \theta_i x_i + \sum_{(i,j)\in E} \theta_{ij} x_{i}x_j ; x_i=1,x_j=0,j \ne i) } {exp(\sum_{i\in V} \theta_i x_i + \sum_{(i,j)\in E} \theta_{ij} x_{i}x_j ; x_i=0,x_j=0,j \ne i )}\\&= log \frac{exp(\theta_i )}{exp (0)}\\&= log exp(\theta_i)\\&= \theta_i\end{aligned}\end{align} \]

通过上式，我们得到了 \(\theta_i\) 的计算方法：

(11.2.7)\[\theta_i = log \frac{p(\mathrm{x}_i=1|\mathbf{x}_{V\backslash \{i\}} = \mathbf{0})}{p(\mathrm{x}_i=0|\mathbf{x}_{V\backslash \{i\}} = \mathbf{0})}\]

我们只需要从观测样本集中先找出除了 \(\mathrm{x}_i\) 以外全部为0的样本子集，然后在分别统计出在这个样本子集中 \(\mathrm{x}_i=0\) 和 \(\mathrm{x}_i=1\) 的样本数量就能计算出 \(\theta_i\) 。

我们令 \(\mathbf{e}_i\) 表示第i个变量为1其它都为0， \(\mathbf{0}\) 表示所有元素都为0， \(\mathbf{e}_{ij}\) 表示第i和j个变量为1其它都为0。那么有：

(11.2.8)\[\theta_i = log p(\mathbf{e}_i) - log p(\mathbf{0})\]

同理可得：

(11.2.9)\[ \begin{align}\begin{aligned}& \ log \frac{p(\mathbf{e}_{ij}) p(\mathbf{0}) }{p(\mathbf{e}_i) p(\mathbf{e}_j)}\\&= log \frac{exp(\theta_i + \theta_j + \theta_{ij})}{exp(\theta_i) exp(\theta_j)}\\&= \theta_{ij}\end{aligned}\end{align} \]

最后参数 \(\theta_{ij}\) 可通过如下方法估计得到。

(11.2.10)\[\theta_{ij} = log p(\mathbf{e}_{ij}) - log p(\mathbf{e}_i) -log p(\mathbf{e}_j) + log p(\mathbf{0})\]

注意，本节所介绍的方法要求观测样本集足够多，公式中的 \(p(\cdot)\) 都是从观测样本中统计得出， 对于任意的i，\(\mathbf{e}_i,\mathbf{e}_j,\mathbf{e}_{ij},\mathbf{0}\) 都有足够的样本才行。

11.2.2. 一般二值变量模型

上一节中，我们限定无向图中的团最多只包含2个结点，实际上这个方法是可以扩展的团大小任意的无向图上。 由于每个团的结点数量不再限定为2，我们用符号 \(\theta_C\) 替代 \(\theta_{ij}\) 表示团上的参数。

对于每个结点变量的独立参数 \(\theta_i\) 还按照 \(\theta_i = log p(\mathbf{e}_i) - log p(\mathbf{0})\) 计算即可。 对于每个团上的参数 \(\theta_C\) 可以通过下式计算：

(11.2.11)\[ \begin{align}\begin{aligned}&\ log p(e_C) - log p(\mathbf{0}) - \sum_{i\in C} \theta_i\\&= log \frac{p(e_C)}{p(\mathbf{0})} - \sum_{i\in C} \theta_i\\&= log \frac { exp(\theta_C + \sum_{i\in C} \theta_i)}{exp(0)} - \sum_{i\in C} \theta_i\\&= \theta_C + \sum_{i\in C} \theta_i - \sum_{i\in C} \theta_i\\&= \theta_C\end{aligned}\end{align} \]