5. 有向图(Directed Graphical Models)¶
我们已经知道多个随机变量组合在一起可以形成联合概率分布,假设有2个二值随机变量(也就是伯努利变量) \((\mathrm{x}_1,\mathrm{x}_2)\) ,这2个随机变量组合成的联合概率分布可以写成 \(p(\mathrm{x}_1,\mathrm{x}_2)\) 。 在离散随机变量的情况下,一种表达联合概率分布的方式是表格表示法,表格中每行代表联合概率分布的一个实例, 比如表格的第一行表示 \(p(x_1=0,x_2=0)=0.2\) 。 这种方式有个很大的缺陷就是:当随机变量的数量n变得很大时,这个表格的规模会指数级增长。假设每个离散随机变量的取值空间大小是 \(r\) ,随机变量的数量是n,则这个表格的规模为 \(r^n\) 。此外对于连续值随机变量无法使用表格的形式。
联合概率分布的另一种表达方式是根据概率论的链式法则(chain rule):联合概率分布可以分解成多个条件概率(local conditional probability)的乘积。
换句话说,可以将多个变量联合概率表示为如下概率的连乘:第一个变量先发生的概率,给定一个后第二个变量发生的概率,给定前两个后第三个变量发生的概率,依次类推。 值得注意的是,可以用任意变量顺序执行这个表达式,结果都是一样的。 链式法则使得我们可以把联合概率分解成一系列条件概率的乘积,但即便如此,当变量数量很多时,仍然是很复杂的, 对于一个条件概率 \(p(\mathrm{x}_n|\mathrm{x}_1,\ldots,\mathrm{x}_{n-1})\) ,它的规模仍然是 \(r^n\) 。
好在我们可以通过引入随机变量的独立性简化条件概率,如果两个变量 \(\mathrm{x}_1\) 和 \(\mathrm{x}_1\) 是相互独立的, 则有:
如果在 \(\mathrm{x}_1\) 已知的条件下, \(\mathrm{x}_2\) 和 \(\mathrm{x}_3\) 是独立的, 既满足条件独立性 \(\mathrm{x}_2 \perp \!\!\! \perp \mathrm{x}_3|\mathrm{x}_1\) ,则有:
如果联合概率中的变量满足独立性或者条件独立性,我们就可以简化链式法则右侧的分解表达式。 比如如果所有变量都是互相独立的,则上述链式法则可以简化成:
综上所述,对于联合概率分布的表达有两点:(1)根据链式法则因子分解成条件概率的乘积;(2)利用变量间的(条件)独立性质简化条件概率(分解因子)。 当我们有了联合概率分布的表达之后,就可以基于此进行一些概率查询,比如后验概率查询、边缘概率推断等等。 然而基于这种代数表达方式,在对联合概率分布进行操作时不是很方便和直观,人们更习惯用图形化的方法去表达和分析一个复杂问题。 那么有没有一种用图形化的方式来表达联合概率分布呢?答案是肯定的,那就是概率图模型(probabilistic graphical models)。
所谓概率图,就是用图形化的方式表示多个随机变量的联合概率分布。概率图一般由结点和边(也叫连接)组成,一个结点表示一个或者一组随机变量, 边表示 变量之间的概率关系 ,结点和边构成图结构。 根据边是否有方向,可以将概率图分为有向图(Directed Graphical Model)和无向图(Undirected Graphical Model)。 有向图又称作贝叶斯网(Bayesian network),无向图又被称作马尔科夫网(Markov network)或者马尔科夫随机场(Markov random fields)。 除了有向图和无向图外,还有一类特殊的图模型–因子图(factor graph),我们在后续的章节中会一一介绍,本章节我们先讨论有向图。
5.1. 有向图¶
一个有向图模型 \(\mathcal{G}\) 包含结点集合 \(\mathcal{V}\) (一个结点表示一个或一组随机变量)和 有向边(有箭头的线段)集合 \(\mathcal{E} \subseteq \mathcal{V} \times \mathcal{V}\) 。 符号 \((i, j) \in \mathcal{E}\) 表示在结点i和j之间存在一条有向边。 一个简单的例子,假设我们有两个随机变量 \(\mathrm{x}\) 和 \(\mathrm{y}\) ,其中随机变量 \(\mathrm{y}\) 依赖随机变量 \(\mathrm{x}\) ,我们用圆圈表示变量(图中结点),用有向边(有箭头)表示变量间的依赖关系,二者组成的联合概率分布可以转化成如下有向图模型。

图 5.1.1 随机变量x和y组成的有向图¶
图中的有向边表示变量 \(\mathrm{x}\) 影响着变量 \(\mathrm{y}\) , 即变量 \(\mathrm{x}\) 是”因”,变量 \(\mathrm{y}\) 是”果” ,或者也可以理解成变量 \(\mathrm{y}\) 依赖于变量 \(\mathrm{x}\) 。 根据这个图二者的联合概率分布可以分解成:
重要
有向图中有向边表达的是变量之间的”单向关系”,即父结点变量影响着子结点变量,一般可以看成是变量间的因果关系、影响关系、条件关系。
在有向图中,联合概率可以分解成每个结点及其父结点组成的条件概率的乘积, 由于每个条件概率的范围是结点及其父结点,不包括更上层的祖先结点,所以一般称作”局部”条件概率(local conditional probability)。 如果一个节点没有父结点,相当于条件概率中没有条件变量,那就是这个变量自己的概率分布。我们再来看一个更一般的情况,下图是由7个随机变量组成的有向图。
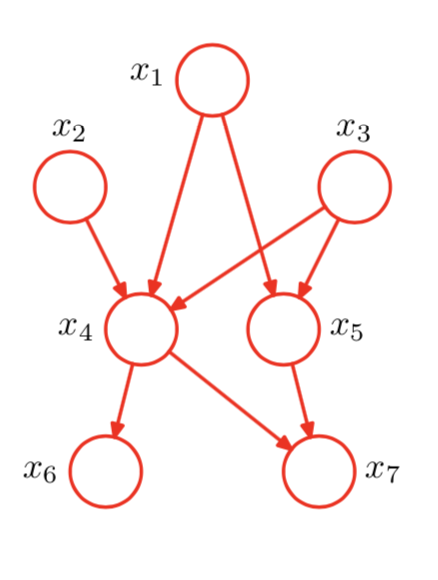
上图7个变量值 \((x_1,x_2,x_3,x_4,x_5,x_6,x_7)\) 的联合概率可以写成:
我们用符号 \(\mathrm{x}_i\) 表示第i个随机变量, 符号 \(\pi_i\) 表示结点i的父结点集合, \(\mathrm{x}_{\pi_i}\) 表示随机变量 \(\mathrm{x}_i\) 所有父结点变量, 当然也可以没有父结点,这时 \(\mathrm{x}_{\pi_i}\) 为空集。 粗体的 \(\mathbf{x}=\{\mathrm{x}_1,\mathrm{x}_2,\ldots,\mathrm{x}_N \}\) 表示所有变量。 那么对于一个一般的有向图,其联合概率分布 \(p(\mathbf{x})\) 的因子分解式为:
我们把 \(p(\mathrm{x}_k|\mathrm{x}_{\pi_i})\) 称为图 \(\mathcal{G}\) 的 局部条件概率(local conditional probability) 。 我们用父子之间的局部关系去构造联合概率分布。 每一个 \(p(\mathrm{x}_k|\mathrm{x}_{\pi_i})\) 都是一个归一化的条件概率分布, 即其每一个可能取值都是一个有效的概率值:非负的并且所有值相加为1。 很容易证明如果这个公式右侧的每一个条件概率分布都是归一化的,那么这个表示方法整体联合概率分布也是归一化的。 用有向图表示多个随机变量的联合概率分布,可以更清晰的表达出变量之间的依赖关系,使得联合概率分布的分解更加清晰和简练。
到这里可能有些读者要问:在有向图中,为什么局部条件概率中的”条件变量”是每个结点的父结点 \(\mathrm{x}_{\pi_i}\) , 而不是其所有祖先结点呢?我们用 \(\mathrm{x}_{\Pi_i}\) 表示结点i的所有祖先变量集合, 即为什么联合概率分布不写成如下形式:
这是因为在有向图中,满足条件独立性 \(\mathrm{x}_i \perp \!\!\! \perp \mathrm{x}_{\Pi_i - \pi_i} | \mathrm{x}_{\pi_i}\) ,所以有 \(p(\mathrm{x}_i|\mathrm{x}_{\Pi_i}) = p(\mathrm{x}_i|\mathrm{x}_{\pi_i})\) 成立。 这就涉及到联合概率分布表达的第二个问题:条件独立性的表示。 概率图模型除了要表达出联合概率分布的因子分解方式,还要同时表达出变量间的条件独立性质。 关于有向图的条件独立性表达在下一节中详细讨论。
一个特定的有向图 \(\mathcal{G}\) 对应着一个因子分解方法, 所有满足这个因子分解方法的联合概率分布都可以用这个有向图 \(\mathcal{G}\) 表示, 我们把符合这个因子分解式的联合概率分布集合称作这个图模型的概率分布族 。 比如 图 5.1.3 ,这是一个6个结点的有向图,每个结点变量是一个伯努利离散随机变量, 我们用表格的方式表示中其中每个局部条件概率分布,表格中每个单元格可以填入一个[0,1]间实数值, 不同的实数值就代表了不同的概率分布实例。换句话说,这个有向图可以代表一类联合概率分布, 只要这些联合概率分布都满足于这个有向图所表示的因子分解方式。
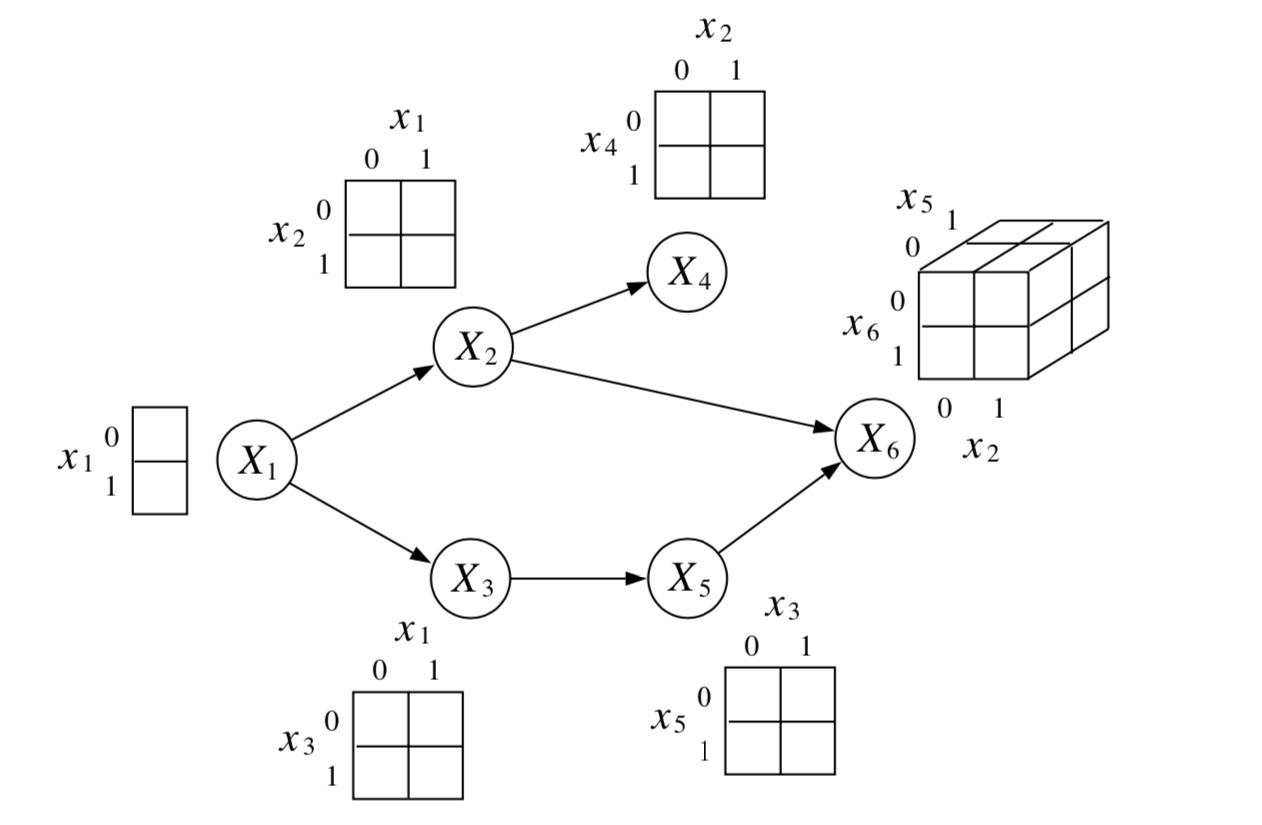
图 5.1.3 用表格表示局部条件概率(local conditional probabilities)。每个结点是一个伯努利变量(01二值变量), 每个表格表示是当前结点及其父结点组成的条件概率分布,每个单元格中都是一个[0,1]间的数值, 并且满足在给定父结点的值时子节点对应的列中的值相加为1。¶
5.2. 条件独立性¶
实现这一特性的关键是 d-separation 的概念。 事实上,贝叶斯网络理论的一个主要贡献是提出了一个表示系统,该系统将(独立)依赖性与图(非)连接性相关联。
联合概率分布表达的另一重要问题就是变量间的条件独立性。我们经常需要知道一个变量集合是否独立于另一变量集合, 亦或者条件独立第三个变量集合,独立性和条件独立性是概率论中非常重要的概念,也是概率图不可或缺的部分, 本节我们讨论有向图如何表达变量间(条件)独立性。
我们知道在有向图中有向边表示变量之间的”因果”关系,能够”直接”影响到结点 \(i\) 的只有其父结点 \(\pi_i\) , 除了父结点以外的其他结点 \(other(i)\) 最多只能”间接”的(通过父结点进行传递)影响到结点i。 从直觉上来讲,如果结点i的所有父结点变量 \(\mathrm{x}_{\pi_i}\) 的取值都已经确定了, 那么显然其他节点 \(other(i)\) 也就无法再影响到变量 \(\mathrm{x}_i\) ,因为其它结点 \(other(i)\) 到结点i的路径已经被”阻断”了。
小技巧
完全独立的两个变量,在图中不会有任何路径连接,就相当于两张独立的概率图了, 也就是说在同一张概率图中不会出现两个完全独立的随机变量,所以在图模型中我们探讨的是条件独立性质。
我们先从典型的三结点有向图开始讨论有向图的条件独立性质。首先是如 图 5.2.1 所示的链式结构, 白色空心结点表示这个变量未知,相反灰色阴影结点表示这个结点变量取值已经确定,换句话说就是我们以阴影结点为条件变量。
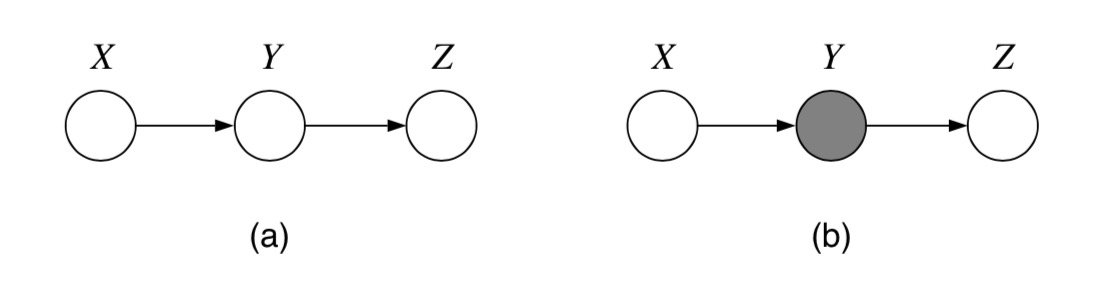
图 5.2.1 链式有向图,父结点已知的条件下,子节点和祖先节点相互独立。¶
根据之前的讨论,当变量Y已知时相当于阻断了X和Z的”联系”,因此我们可以得到条件独立性质 \(\mathrm{X} \perp \!\!\! \perp \mathrm{Z} | \mathrm{Y}\) 。 这种情景我们可以扩展成在父结点 \(\mathrm{x}_{\pi_i}\) 的条件下子节点 \(\mathrm{x}_i\) 和其祖先节点 \(\mathrm{x}_{\Pi_i-\pi_i}\) 相互独立 \(\mathrm{x}_i \perp \!\!\! \perp \mathrm{x}_{\Pi_i-\pi_i} | \mathrm{x}_{\pi_i}\) 。
第二类典型结构是如 图 5.2.2 所示的结构,这种结构探索的是同一个父结点下子结点之间的独立性关系, 根据”阻断”理论,容易的出 \(\mathrm{X} \perp \!\!\! \perp \mathrm{Z} | \mathrm{Y}\) 是成立的。 换句话说就是在父结点已知的条件下,子节点之间相互独立。

图 5.2.2 在父结点已知的条件下,子节点之间相互独立。¶
第三类图形是如 图 5.2.3 所示的V-型结构,这个结构的有向图比较特殊,在这个结构下我们探索的是 在 子结点的条件下父结点之间的独立性问题 。在这个结构下,X与Z是 条件不独立 的,相反两者是 边缘独立 的。 我们可以把X和Z想象成红尘中的男男女女,在没有任何一个孩子时,这些男男女女都是独立的个体,互相间没有确定性的关系,是互相独立的。 然后如果跑出来一个”小孩子”(子结点的条件下),那么这个小孩子的”父母”(父结点)也就昭然若揭了,父母间一定存在了某种羞羞的关系, 父结点间就不在独立。所以 在有向图中子结点的条件下父结点不独立 。
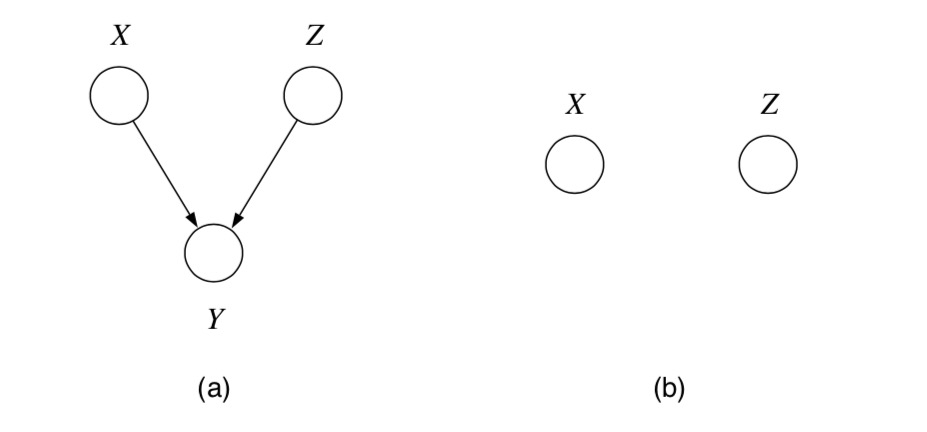
图 5.2.3 有向图的V-型结构,X与Z不再条件独立,而是边缘独立。¶
至此,我们已经探讨完三个典型有向图结构的条件独立性质。 在更复杂的有向图中判断条件独立性的方法是贝叶斯球算法,这里不再介绍,有兴趣的读者可以参考其他资料。
5.3. 本章总结¶
概率图是联合概率分布的图形化表示,其中结点表示变量,结点之间的边表示变量之间的关系, 有向图中的有向边表示了变量之间的单向关系,可以看做是”因果(依赖)”关系。 一个概率图模型需要表达两个方面的内容:(1)联合概率分布分因子分解表达方式;(2)变量间的条件独立性质。
有向图的表达的联合概率因子分解方式为:局部条件概率的乘积 \(p(\mathbf{x}) = \prod_{i=1}^N p(\mathrm{x}_i|\mathrm{x}_{\pi_i})\) 。 有向图的条件独立性可以概括为:在所有父结点的条件下,结点i与其它结点条件独立。 \(\mathrm{x}_i \perp \!\!\! \perp \mathrm{x}_{other(i)-\pi_i} | \mathrm{x}_{\pi_i}\)
一个特定的图模型代表了一个联合概率分布族,这个族中的联合概率分布必须满足这个图的因子分解方式以及图中隐含的条件独立性质。 有向图模型表示将一组变量上的联合概率分布分解为局部条件概率分布的乘积的一种分解方式。 有向图模型也定义了一组条件独立性质,根据图进行分解的任何概率分布都必须满足这些条件独立性。