6. 无向图(Undirected Graphical Models)¶
有向图表达是变量之间的关系是单向关系,即一个影响另一个,比如因果关系。 但很多时候变量之间的关系是互相影响的,这时候有向图将不是那么方便了。 本章我们讨论概率图模型的另一类图模型–无向图模型。 和有向图类似,我们对无向图的讨论,包括图模型的因子分解方式和条件独立性的表达。
6.1. 无向图的定义¶
一个无向图模型(Undirected Graphical Model),又被称为马尔科夫随机场(MRF,markov random field), 也可以被称为马尔科夫网络(Markov network)。和有向图一样,图中的结点对应着随机变量,边(edge)对应着变量之间的关系, 不一样是的无向图中边是没有方向(没有箭头)的。一个无向图模型是这样一个图 \(\mathcal{G}=(\mathcal{V}, \mathcal{E})\) ,\(\mathcal{V}\) 表示图中的结点(随机变量)集合, \(\mathcal{E} \subset \mathcal{V} \times \mathcal{V}\) 表示图中无向边集合。
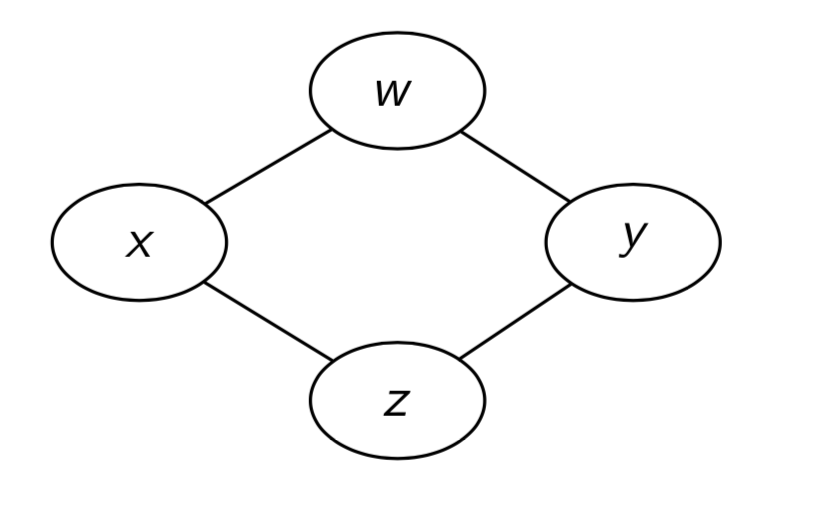
图 6.1.3 一个无向图¶
重要
有向图中的有向边表示两个变量的依赖关系,这种关系可以看成是因果、影响、依赖等等,是一个影响着另一个,对应着条件概率 。 而在无线图中,无向边表示两个变量的一种互相关系,互相影响,互相软限制等等,不再是条件概率 。
无线图中的无向边表示变量间的”互相关系”,有时一些变量间互相影响会形成一个”团(clique)” 。 一个 团(clique) 是图中一个全连接的结点子集,团中任意两个结点间都有边相连接。 一个 最大团(maximal clique) 是一个不能再增加结点的团,最小的团就是图中一条边连接的两个结点组成的团。

图 6.1.4 一个包含4个结点的无向图,绿色圈的时一个团,蓝色圈是一个最大团。¶
如 图 6.1.4 ,绿色圈中的是一个团,蓝色圈中的是一个最大团,一个结点可以包含在多个团中, 一个无向图总是可以划分为很多个团的集合。
6.2. 条件独立性¶
与有向图一样,无向图也表示一个分解方式,同时也表示一组条件独立关系。 无向图上条件独立的表达和有向图有些类似,也是从”路径阻断”的角度去表达。

图 6.2.2 左(a) 表达条件独立属性 \(\mathrm{x}_{A} \perp \!\!\! \perp \mathrm{x}_{B} | \mathrm{x}_{C}\) 的无向图。 右(b) 当移除阴影结点后,原图被分裂成多个连接子图,导致A和B成为不相交的两部分。¶
我们把图中的结点分成三组:A,B,C,每组中的变量集合分别用 \(\mathrm{x}_{A},\mathrm{x}_{B},\mathrm{x}_{C}\) 表示。 如果A中结点和B中结点的所有路径都经过C,我们说C可以阻断A和B的联系,那么就满足条件独立性质:
\(\mathrm{x}_{A} \perp \!\!\! \perp \mathrm{x}_{B} | \mathrm{x}_{C}\) ,C把整个图分割(separation)成A、B两部分。
另一种检测条件独立性的方法如下:从图中删除C中的所有节点,以及与这些结点关联的任何边。如果不再存在从A中任意结点到B中任意结点的路径, 那么 \(\mathrm{x}_{A} \perp \!\!\! \perp \mathrm{x}_{B} | \mathrm{x}_{C}\) 。
我们用符号 \(N(i)\) 表示结点i的所有邻居结点,用符号 \(other(i)\) 表示与结点i没有直接相连接的结点(非邻居结点), 那么在无向图中有 \(\mathrm{x}_{i} \perp \!\!\! \perp \mathrm{x}_{other(i)} | \mathrm{x}_{N(i)}\) 成立。 我们看到,无向图很自然地的表示出了变量间的条件独立性质。需要注意的一点时, 在无向图的一个团(clique)中,任意两个结点都是存在边的,换句话说一个团中的结点都是互为邻居的, 也就是说 同一个团中的结点间不存在(条件)独立性 。
6.3. 图的分解¶
根据概率论中的链式法则,联合概率分布可以分解成”局部函数”的乘积形式”。 局部函数的领域范围表示这些结点变量之间存在”关系”,局部函数的具体内容表示这种”关系”是什么。 在有向图中,这个”局部函数”的定义范围是结点i及其父结点集合 \(\mathrm{x}_{\pi_i}\) 组成的领域, 函数的”具体内容”是条件概率 \(p(\mathrm{x}_i|\mathrm{x}_{\pi_i})\) , 也就是说有向图的因子分解是建立在 局部条件概率 上的。 现在我们讨论无向图的因子分解方式,同样我们也需要确认两个事情:a. 局部函数的定义域(范围)”local”; b.局部函数的内容。
在无向图中,一种直觉上的想法是用每个结点及其邻居结点组成的条件概率 \(p(\mathrm{x}_i|\mathrm{x}_{N(i)})\) 表示”局部函数” ,但这种方式是存在问题的。 在无向图中,结点是互为邻居的,这种方式无法确保不同结点的条件概率一致性(如果无法理解,只需记住这样不可行)。 另一种可能的想法是用边缘概率表示这个”局部函数”,即无向图的因子分解式定义成一系列边缘概率的乘积。 我们可以通过一个简单的例子证明这也是不可行的。
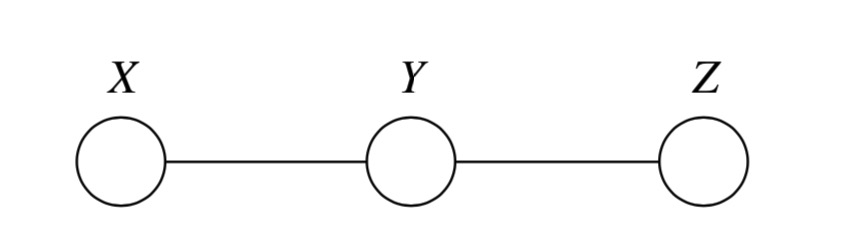
图 6.3.1 三结点的链式无向图,满足条件独立性 \(\mathrm{X} \perp \!\!\! \perp \mathrm{Z}|\mathrm{Y}\)¶
考虑 图 6.3.1 所示的三结点无向图,这个无向图模型满足条件独立性 \(\mathrm{X} \perp \!\!\! \perp \mathrm{Z}|\mathrm{Y}\) , 根据这个条件独立性以及链式法则可得:
此外,图中有两个团 \(\{X,Y\}\) 和 \(\{Y,Z\}\) ,我们可以把前两个因子乘在一起得到第一个团的边缘概率 \(p(x,y)\) ,这样此模型的因子分解式就变成 \(p(x,y,z)=p(x,y)p(z|y)\) 。 亦或者我们把 \(p(y)\) 和 \(p(z|y)\) 乘在一起,模型的因子分解式就变为 \(p(x,y,z)=p(x|y)p(z,y)\) 。 但不管怎样都不能把无向图的联合概率分布分解成边缘概率乘积的形式,即 \(p(x,y,z) \neq p(x,y)p(z,y)\) 。
核心问题是解决这个”局部(local)函数”的领域(即涵盖的结点范围)和内容:本质上就是在无向图中这个”局部(local)”的含义! 这里我们利用上节讨论的条件独立性来尝试解决这个问题。考虑无向图中两个没有边的两个结点 \(\mathrm{x}_i,\mathrm{x}_j\) , 根据条件独立性质,在给定其他所有结点 \(\mathrm{x}_{rest}\) 时, 这两个结点一定是条件独立的 \(\mathrm{x}_i \perp \!\!\! \perp \mathrm{x}_j|\mathrm{x}_{rest}\) ,因为这两个结点间没有可达路径。 其中 \(\mathrm{x}_{rest}\) 表示图中除去 \(\mathrm{x}_i\) 与 \(\mathrm{x}_j\) 之外的其它所有结点,则有:
这意味着,我们一定有某种方法,在无向图的联合概率因子分解表达式中,将 \(\mathrm{x}_i\) 和 \(\mathrm{x}_j\) 分别放到不同的因子中,换句话说,我们的”局部函数”中不会同时包含 \(\mathrm{x}_i\) 和 \(\mathrm{x}_j\) 。 回顾一下,无向图中的一个团表示的是一个全连接子图,即团中任意两个结点都有边连接,也就是说同一个团中的结点绝对不满足条件独立性的。 而不同团之间的结点是可以有条件独立性的,这就意味着我们的”局部函数”的定义范围就是图中的团即可。 结论就是,无向图表示的联合概率分布可以分解成定义在团上的局部函数的乘积, 我们将这个局部函数称为势函数(potential function)。
给定一个无向图及其变量集合 \(\mathrm{x}_1,\dots,\mathrm{x}_N\) , 其中的最大团集合为 \(\mathcal{e}\) ,定义联合概率分布表达式为:
有向图的因子分解式中每个因子是一个条件概率,是归一化的概率分布,所有因子的乘积也是归一化的概率,所以不再需要一个配分函数。 然而在无向图中的因子分解中,每个因子函数(势函数)不再是有效的概率形式,其连乘的结果同样不具有概率意义, 所以需要一个归一化系数来保证最后输出的是有意义的概率值。 在这个表达式中,\(Z\) 被称为”配分函数(partition function)” ,是归一化系数, 其作用是使得对应于所有联合分配的概率总和为1(其实就是所有分子的可能取值的求和,为了保证最终输出的是概率值)。 配分函数 \(Z\) 可以被写成(所有分子的可能取值的求和):
这个求和操作通常是难以计算的,甚至无法计算。 幸运的是,对于许多场景下,例如”条件概率查询”或者”最大概率查询”,我们不需要计算它。 对于其他计算,例如学习参数 \(\psi\) ,我们确实需要它。如果不理解没关系,后续章节内容会相信说明。
函数 \(\psi\) 可以是任意 非负值 的函数(i.e. 不需要保证求和是1) ,是定义在最大团块的变量上的势函数(potential function), 有时也被称为兼容性函数(compatibilities) 。我们用这个函数去表示因子分解中的局部函数,这个”局部”的范围我们已经讨论完毕, 是定义在(最大)团上的,下一步我们讨论这个函数的具体形式(内容)。
备注
事实上,势函数并不是一定要定义在图中的最大团上,定义在图中最大团的子团上也是成立的。
势函数的解释
我们已经知道,无向图中势函数既不是条件概率也不是边缘概率,并没有局部概率的解释。 我们回想一下,根据链式法则,联合概率可以分解成一系列局部函数的乘积形式,等价于因子分解的过程,所以也可以把这个过程称为因子分解。 在有向图中这个局部函数是局部条件概率,在无向图中这个局部函数是势函数。 局部函数的隐含意义是其包含的变量之间的关系,所以势函数表达的也是变量的之间的关系。 这种关系我们可以理解成是变量之间的”同意”、”约束”、”能量”等等,总之是变量之间的一种直接的相互关系, 并不强制要求是有意义的概率关系(这点和有向图不同)。但这些势函数的乘积组成的联合概率需要具有概率意义,所以有了一个配分函数Z。
鉴于此,我们对势函数并没有特别的形式上的要求,但是必须 非负的 (连乘的结果需要符合概率意义,所以必须是非负的), 此外 同一个无向图中不同团上的势函数可以具有不同的形式。 当团上的变量取得不同值时(团上变量发生变化),对应势函数输出不同的值,输出的值越大,归一化后的概率值就越大。 除此之外并没有其它要求,只需要根据具体实际场景中变量之间的关系去定义势函数即可。
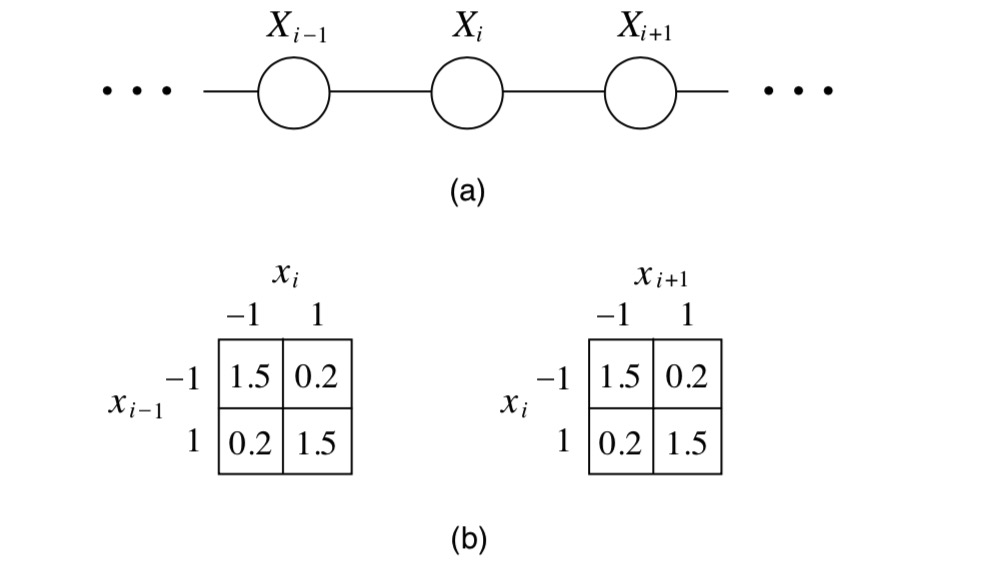
图 6.3.2 伯努利变量的链式无向图,相邻两个结点势函数的表格形式。¶
如 图 6.3.2 (a),考虑一个二值伯努利离散随机变量组成的链式无向图,\(\mathrm{x}_i \in \{-1,1\},i=0,\ldots,n\) , 在物理学中,这种模型用于模拟晶体的磁性行为,其中二元变量具有磁性“旋转”的解释。 其中相邻的晶体(结点)收到磁场的相互影响,更倾向于用于一样的磁性状态,比如当 \(\mathrm{x}_i=1\) 时,其邻居 \(\mathrm{x}_{i-1},\mathrm{x}_{i+1}\) 受到影响也倾向于为1。 我们可以简单的用势函数表达这种关系,如 图 6.3.2 (b),邻居结点(团 \(\{\mathrm{x}_{i-1},\mathrm{x}_{i}\}\)) 拥有一致”行为”的”能量值”更高一些1.5, 反之赋予低的”能量值”0.2,高能量值归一化后的概率值更高。
既然势函数一定要是非负的,所以通常情况下,我们将势函数 \(\psi\) 表示为指数函数形式(满足一定是非负的),即:
其中函数 \(E(x_C)\) 是一个任意的实数值函数,不再要求非负。 在统计物理学中, \(E(x_C)\) 被称为能量函数(energy function),表示状态 \(\mathbf{x}_C\) 的能量(energy)。指数函数的另外一个优势就是指数的连乘容易操作,连乘可以转换成指数求和。 无向图联合概率分布的分解可以改写成:
提示
了解玻尔兹曼分布(Boltzmann distribution)的读者可以发现,无向图的联合概率分布的表达式就是玻尔兹曼分布。
在同一个无向图中,不同团上的势函数可以有不同的形式,即不同团可以拥有不同的势函数 。此外,在很多场景中, 无向图的联合概率表达中不经包含团上的势函数,也可以加入单个结点的势函数。
6.4. 有向图 vs 无向图¶
我们已经看到有向图自然地表示分解属性,并且无向图自然地表示条件独立性属性。 这是否意味着当我们有条件概率分布时,我们应该总是使用有向图;当我们有条件独立性时,我们应该总是使用无向图? 不是这样的,两类图形各有自己的优劣,是不同的模型工具,分别适合不用的应用场景。
通常情况下,有向图和无向图并不能完全等价的进行转换(两者拥有相同的条件独立性)。举个例子,考虑如下图模型。

让我们尝试构造一个有向图来表示相同的分布族(即拥有同一组条件独立性)。 首先,注意到至少要和无向图拥有同样的边集合,因为任何由边连接的变量都相互依赖,无论是否观察到任何其他变量。 为了使图形无环,其中一个节点必须在拓扑排序中排在最后; 不失一般性,让我们假设它是节点z。 然后z有两个入边,无论我们如何设计剩余的另两条边的方向, 我们都无法保证得到 \(\mathrm{x} \perp \!\!\! \perp \mathrm{y} | \mathrm{w}, \mathrm{z}\) (但是这在无向图中却是满足的)。 因此没有办法能满足同样的条件独立性的前提下把上述无向图转换成有向图。
那么,反过来,我们可以在保证原有条件独立性的前提下,把任意的有向图转换成无向图吗?不能,v型结构的有向图就不行。
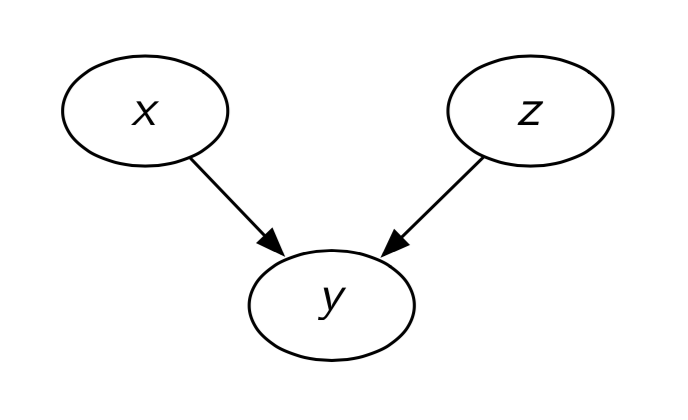
图 6.4.1 v型结构的有向图¶
在上一章节我们讲过,在v型有向图中满足边缘独立 \(\mathrm{x} \perp \!\!\! \perp \mathrm{z}\) , 但是不满足条件独立 \(\mathrm{x} \perp \!\!\! \perp \mathrm{z}|\mathrm{y}\) 。 相比之下,无向图形模型具有某种单调性属性:当观察到额外的节点时,新的条件独立性集合是旧的条件独立性的严格超集。 因此,没有无向图可以表示与v结构相同的分布族。
然而,我们还是可以把一个有向图转换为无向图的,当然转换后条件独立性会发生变化,这是通过”道德化(moralization)”来实现的。
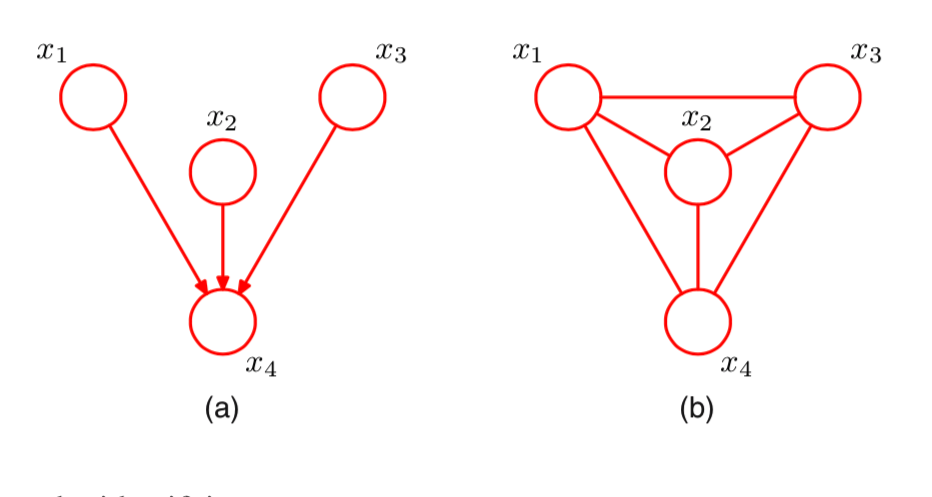
图 6.4.2 (a)一个简单的有向图;(b)对应的道德图。¶
道德化(moralization):首先完全连接每个结点的父母,然后删除图中箭头的方向。 道德化通过将父母连接在一起来“联姻”父母。 有关示例,请参见 图 6.4.2 ,这种”父结点之间结婚”的过程被称为道德化或者伦理化(moralization), 去掉箭头后生成的无向图被称为道德图(moral graph)。很重要的一点是,在这个例子中道德图是完全链接的,因此没有表达出条件独立性质。
因此,通常为了将有向图转换为无向图,我们首先在图中每个结点的所有父结点之间添加额外的无向边,然后去掉原来有向边的箭头, 得到道德图。之后,我们将道德图的所有团块势函数初始化为1。接下来,我们拿出原始有向图中所有条件概率分布因子,将他们乘到一个团块势函数中去。 由于伦理步骤的存在,总会存在至少一个最大团块,包含因子中的所有变量。注意,在所有情形下,配分函数都为Z=1。
提示
我们看到从一个有向图转化为无向图的过程中,我们必须从图中丢弃掉一些条件独立性质。 当然,通过简单的使用全连接的无向图,我们可以很容易的将有向图上的任意概率分布转化为无向图上的概率分布。 但是,这会丢掉所有的条件独立性质,因此没有实际意义。而”伦理”过程增加了最少的额外链接,因此最大可能的保证了条件独立性质(注意,还是会有损失的)。
6.5. 树¶
这里我们先介绍一类特殊的图形结构–树,如果不是很理解也没关系,后续用到的章节中会详细讨论。
在无向图的情形中,树被定义为满足下面性质的图:任意一对结点之间有且只有一条路径。这样的图没有环。 在有向图的情形中,树的定义为:有且仅有一个没有父结点的结点,被称为根(root),其它所有结点都只有一个父结点。
如果我们将有向树转换为无向图,我们会看到在”伦理”步骤不会增加任何边,因为所有结点最多只有一个父结点,从而对应的道德图是一个无向树。 无向树和有向树的例子如 图 6.5.1 (a)和 图 6.5.1 (b)所示。注意,一个表示为有向树的概率分布可以很容易的转化为一个由无向树表示的概率分布,反之亦然。 如果有向图中存在具有多个父结点的结点,但是在任意两个结点之间仍然只有一条路径(忽略箭头方向),那么这个图被称为”多重树(polytree)”。 如 图 6.5.1 (c)所示。这样的图存在多个没有父结点的结点,一些结点亦存在多个父结点,对应的道德无向图会存在环。
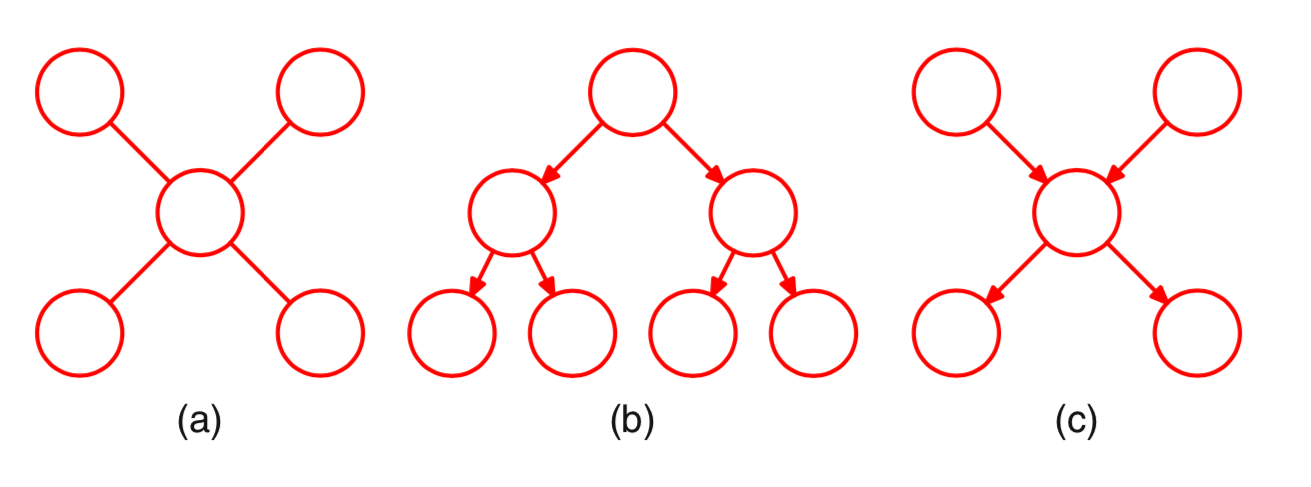
图 6.5.1 (a)一个无向树;(b)一个有向树;(c)一个有向多重树(polytree)¶
6.6. 本章总结¶
一个图模型是一类概率分布族的图形化表达。一个图模型需要表达两种信息:因子分解方式和条件独立性。 在某种意义上,有向图更自然地直接表示条件概率,而无向图更自然地表示条件独立性属性。