1. 文本去重

1.1. 背景

最近有两个项目需要文本去重功能，一个是知识库，一个是话术库。 两个场景非常相似，都是在内容录入的时候检查一下库中是否已经存在相似的内容， 如果不存在直接写入即可。 若存在需要反馈相似的内容列表，由录入者决定是继续录入，还是放弃。

无论是知识库，还是话术库，内容主题都是都是中文文本，二者在文本的长度和规模上略有差异，但应该都不会很大。 规模方面，知识库应该在万级别，话术库在千级别。 文本长度方面，话术一般也就百十字，知识库的内容可能略长一些，总体来看都不会太长。

需求是开发一个查重服务，在录入新内容时检测库中是否已经存在类似的内容。 这个功能虽然不复杂，但秉着严谨的态度，我们还是做了一些技术调研， 先整理一下行业内流行的技术方案，然后在针对我们的场景做针对性的技术方案。 本文前半部分是行业内相关的一些技术综述，后半部分是针对我们的场景做的技术方案。

1.2. 技术思路

我们首先理一下整个技术思路。

对于文本去重，显然最核心的一点是计算文本间的相似度。 关于相似度的计算，在我们的场景下，并不需要语义层面的理解，只考虑文字层面的相似性即可， 这极大的简化了我们的工作。关于相似（距离）计算的方法有很多，稍后我们会给出常见相似度计算的方法。

虽然相似计算并不复杂，但是当文本长度和数量规模增大以后，这对算法的性能带来极大挑战， 所以我们难点是在 大规模下的性能问题 ，一般有两个思路来解决这个问题。

1. 降低相似度算法的复杂度，提高匹配速度，以满足大规模下的性能需求。

2. 类似于推荐场景，可以分成粗略匹配和精细匹配两个阶段。 首先是性能高但精度差的粗略匹配，这一步要求匹配效率高，精度可以差一些，目的是缩小数据规模。 然后才是小规模数据下的精确匹配。

以上两种方法并不冲突，我们可以在两个方向都进行改进。 行业内有很多相关的技术方案， 下面先给出行业内流行的一些技术， 最后讨论下针对我们场景的方案。

1.3. 相似（距离）算法

我们首先回归一下常见的距离算法，定义符号 \(x\) 和 \(y\) 表示两个向量， \(d\) 表示两个向量的距离或者相似度。

1.3.1. 欧氏距离（Euclidean Distance）

欧氏距离，又名欧几里德距离，是最常见的向量距离，定义为

(1.3.17)\[d = \sqrt{\sum_{i}^n (x_i - y_i)^2}\]

欧几里德距离就是两个向量空间中两个点之间的直线距离。

1.3.2. 闵科夫斯基距离（Minkowski Distance）

(1.3.18)\[d = \sqrt[p]{\sum_{i}^n (x_i - y_i)^p}\]

显然闵科夫斯基距离是欧氏距离的扩展。

1.3.3. 曼哈顿距离（Manhattan Distance）

曼哈顿距离的定义为：

(1.3.19)\[d = \sum_{i}^n |x_i - y_i|\]

从公式可以看出，曼哈顿距离就是两个向量每个维度上差值的求和。

曼哈顿距离和欧几里得距离的区别就是：

• 欧几里得距离是向量空间中两个点的直线距离

• 曼哈顿距离是向量空间中每个维度差值的总和

我们从维基百科拉过来一张图，就可以很直白的看到这二者的区别， 假设在下方棋盘一样的图示中，白色方块表示为建筑物，灰色线条表示为道路， 那么其中绿色线路表示为黑色两点之间的欧几里德距离（两点之间直线最短）， 而剩下的红蓝黄三色线路表示的均为为曼哈顿距离：

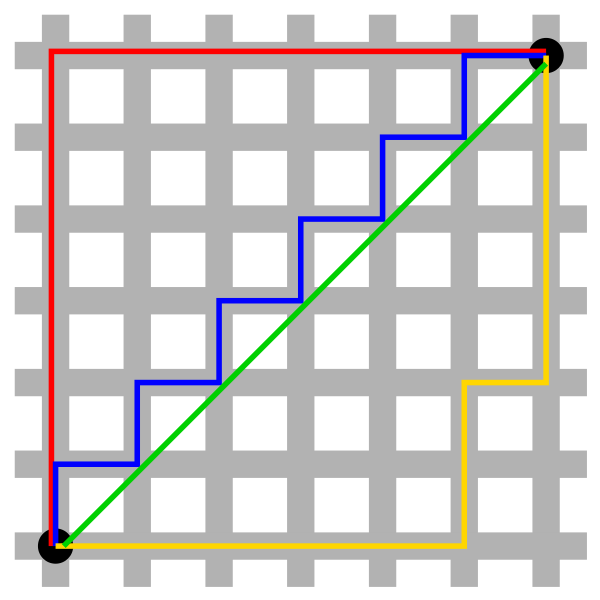
图 1.3.1 二维空间的曼哈顿距离

1.3.4. 切比雪夫距离（Chebyshev Distance ）

Chebyshev distance 得名自俄罗斯数学家切比雪夫，切比雪夫距离的定义为：

(1.3.20)\[d = max(|x_i,y_i|)\]

意思就是，x 和 y 两个向量，对应元素之差的最大值的绝对值。

1.3.5. 马氏距离(Mahalanobis Distance)

(1.3.21)\[d = \sqrt{(x-y)^T S^{-1} (x-y)}\]

其中 \(S\) 是 \(x\) 和 \(y\) 的协方差。

1.3.6. 余弦夹角相似度(Cosine Similarity)

余弦夹角相似度是两个向量夹角的余弦值，计算公式为

(1.3.22)\[cos \theta = \frac{x \cdot y}{||x|| \times ||y||}\]

两个向量的夹角 \(\theta\) 的范围是 \([0,180]\) ，其余弦值得范围是 \([-1,1]\),

• \(cos \theta <0\) 意味着两个向量方向相反。

• \(cos \theta =0\) 意味着两个向量方向垂直，一般看作不相关。

• \(cos \theta >0\) 意味着两个向量方向同向。

1.3.7. 汉明距离（Hamming Distance）

海明距离，又名汉明距离，为两串向量中，对应元素 不一样的个数。 比如 101010 与 101011 的最后一位不一样，那么汉明距离即为1,， 同理 000 与 111 的汉明距离为3。

但这没有考虑到向量的长度，如 111111000 与 111111111 的距离也是3， 尤其是比较文本的相似时，这样的结果肯定不合理，因此我们可以用向量长度作为分母。 Python 中的 hamming distance 即这么计算的。

汉明距离也是值越小越相似，但除以长度之后的海明距离， 最大值为1（完全不相似），最小值为0（完全一致）。

小技巧

如果两个向量长度相同，汉明距离可以是异或运算结果中1的个数。

1.3.8. Jaccard 系数

Jaccard 系数计算的是两个集合的相似性， 两个集合中，交集的个数/并集的个数。

定义集合A和B的的 Jaccard 系数为

(1.3.23)\[\frac{|A \cap B|}{ |A \cup B|}\]

假设有如下集合，

(1.3.24)\[ \begin{align}\begin{aligned}S_1 &= \{ 1,2,5\}\\S_2 &= \{ 3\}\\S_3 &= \{ 2,3,4,6\}\\S_4 &= \{ 1,4,6\}\end{aligned}\end{align} \]

集合 \(S_1\) 和 \(S_3\) 之间的 Jaccard similarity 为

(1.3.25)\[\mathop{JS}(S_1,S_3) = \frac{|\{ 2 \}|}{ | \{ 1,2,3,4,5,6\}| } = \frac{1}{6}\]

当处理文本时，两个集合可以是两个文本的 字 集合，也可以是分词后的 词 集合， 如果词集合太大，也可以先用 TF-IDF 筛选出比较重要的关键词作为词集。

Jaccard系数和汉明距离类似的，只不过汉明距离考虑位置信息，而Jaccard系数不考虑位置。

1.3.9. 编辑距离

设有字符串A和B，B为模式串，现给定以下操作：

• 从字符串中删除一个字符；

• 从字符串中插入一个字符；

• 从字符串中替换一个字符。

通过以上三种操作，将字符串A编辑为模式串B所需的最小操作数称为A和B的最短编辑距离，记为ED(A,B)。

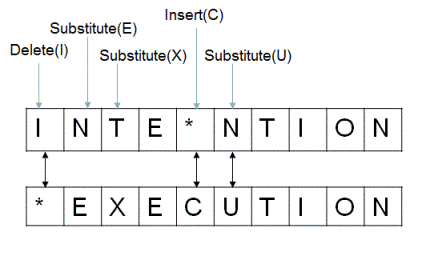
图 1.3.2 编辑距离

1.3.10. 最长公共字串

最长公共子串（Longest Common Substring）： 是指两个字符串中最长连续相同的子串长度。

1.3.11. 最长公共子序列

(Longest Common Subsequence, LCS)

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入： text1 = “abcde”, text2 = “ace”

输出： 3

解释： 最长公共子序列是 “ace” ，它的长度为 3 。

小技巧

最长公共子串（Longest Common Substring）与最长公共子序列（Longest Common Subsequence）的区别： 子串要求在原字符串中是连续的，而子序列则只需保持相对顺序，并不要求连续。

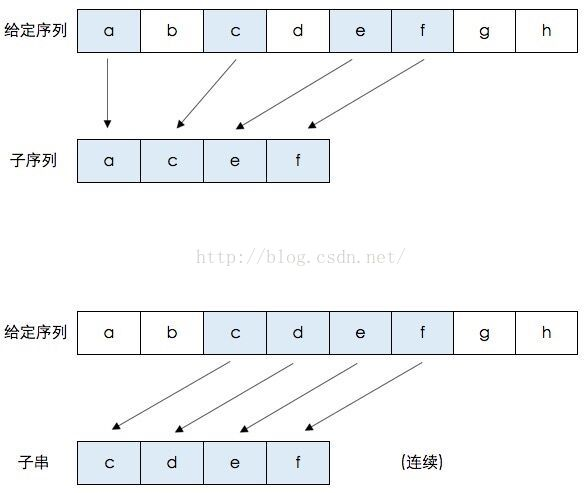
图 1.3.3 子序列和子串

1.4. 文本去重

在文本去重这个场景，我们无需关注语义，只需要关注文字上是否相似即可， 因此上述众多相似度算法中，Jaccard similarity 是最合适的， 如果有文档内容对比标红的需求，可以用 最长公共子序列 实现。

• 判断文档相似度：Jaccard similarity

• 重复部分标红：最长公共子序列

在数据规模较小时，上述方案没有问题，但是当面临超大规模的数据时， Jaccard similarity 在空间和时间上都会存在瓶颈。

1.4.1. KShingle算法

首要的一个问题是如何把一篇文档转换成一个集合，K-shingle` 就一种利用滑动窗口对文档进行切片， 切片后的片段组成集合作为这篇文档的特征集合。

对于一篇文档而言， K-shingle 定义为文档中 连续 的 \(K\) 个词汇组成的词组，也可以叫做 K-gram， 就是用长度为 \(K\) 的滑动窗口按顺序扫描文档，得到的片段（长度K）就是这篇文档的 K-shingle， 所有的片段组成的集合作为这篇文档的特征集合.

最后通过计算两个文档的 K-shingle 集合的 Jaccard similarity 作为两个文档的相似度。

思考

直接只用文档的词集合不行么？为什么还要 K-shingle ?

K-shingle 的意义，可以多少保留一点词序信息，但个人感觉意义不大。

1.4.2. Minhash算法

Jaccard similarity 看上去很简单，但是当文档比较长时，文档的特征集合比较大，尤其是 K-shingle 集合一般比较大，此时就可能面临时间和空间的双重瓶颈。

此时一个思路就是减小文档特征集合的大小，以此加速 Jaccard similarity 的过程。 Minhash 就是这个思路，利用 hash 加随机的方式减少文档特征集合的大小。 这样的操作一定是有损的，因此 Minhash 是 Jaccard similarity 的一种近似估计。

算法过程:

1. 令 \(h\) 表示一个 hash 函数，它可以把词集 \(V\) 中的任意一个元素映射到一个唯一整数（这里忽略冲突问题）。

2. 对集合 \(S\) 中的每个元素用 \(h\) 映射到一个整数。

3. 定义 \(h_{min}{S}\) 表示集合 \(S\) 中所有元素 hash 值最小的那个 元素 ，这就是算法名字的由来。

4. 重复上述步骤 \(k\) 次（注意每次要选择不一样的 hash 函数），得到 \(k\) 个 \(h_{min}{S}\) 的序列就作为文档 \(S\) 新的签名（特征集合）

5. 文档之间新签名集合的 Jaccard similarity 作为文档间相似度。

hash 函数可以选择如下的函数， 其中 \(a\) 和 \(b\) 可以随机得到，不同的 \(a\) 和 \(b\) 表示一个不同的 \(h(x)\) 。\(c\) 是一个大于 \(max(x)\) 的 质数。

(1.4.18)\[h(x) = (a x +b)% c\]

备注

感觉就是对每个集合 \(S\) 中的元素进行了一个随机负采样！显然这只能作为文档原始 Jaccard similarity 的一个近似估计值。

1.4.3. simhash

本节内容转自： https://www.cnblogs.com/maybe2030/p/5203186.html

SimHash 是 google 用来处理海量文本去重的算法。 SimHash 可以为一个文档生成成一个 64 位的签名（或者指纹）。 判断文档是否重复，只需要判断文档签名之间的汉明距离。 根据经验，一般当两个文档签名之间的汉明距离小于 3，就可以判定两个文档相似。

算法过程:

1. 分词，把长文本进行分词，去掉停用词后得到词的集合。然后为每个词加上权重，我们假设权重分为5个级别（1~5）。 比如：“ 美国“51区”雇员称内部有9架飞碟，曾看见灰色外星人 ” ==> 分词后为 “ 美国（4） 51区（5） 雇员（3） 称（1） 内部（2） 有（1） 9架（3） 飞碟（5） 曾（1） 看见（3） 灰色（4） 外星人（5）”， 括号里是代表单词在整个句子里重要程度，数字越大越重要。

2. hash，通过hash算法把每个词变成hash值，比如“美国”通过hash算法计算为 100101,“51区”通过hash算法计算为 101011。

3. 加权，通过 2步骤的hash生成结果，需要按照单词的权重形成加权数字串，比如“美国”的hash值为“100101”，通过加权计算为“4 -4 -4 4 -4 4”；“51区”的hash值为“101011”，通过加权计算为 “ 5 -5 5 -5 5 5”。

4. 合并，把上面各个单词算出来的序列值累加，变成只有一个序列串。比如 “美国”的 “4 -4 -4 4 -4 4”，“51区”的 “ 5 -5 5 -5 5 5”， 把每一位进行累加， “4+5 -4+-5 -4+5 4+-5 -4+5 4+5” ==》 “9 -9 1 -1 1 9”。这里作为示例只算了两个单词的，真实计算需要把所有单词的序列串累加。

5. 降维，把4步算出来的 “9 -9 1 -1 1 9” 变成 0 1 串，形成我们最终的 SimHash 签名。大于0的位记为1， 小于0的位记为 0。最后算出结果为：“1 0 1 0 1 1”。

整个过程的流程图为：

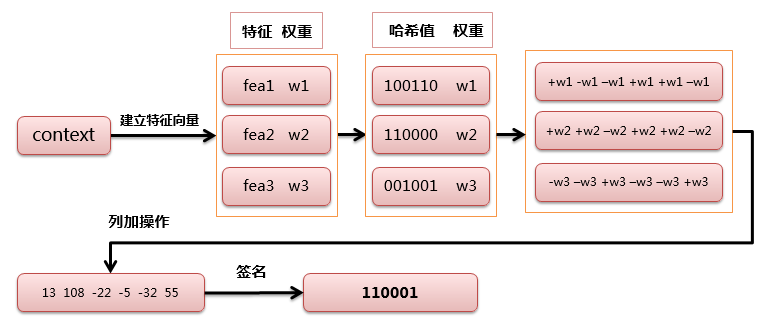
图 1.4.1 SimHash 算法过程

每篇文档算出签名S后，再计算两个签名的汉明距离，汉明距离是这两个二进制数异或后1的个数。 根据经验，对于64位的 SimHash ，汉明距离在3以内的都可以认为相似度比较高，认为这两个文档基本相同。 根据这个特点，可以把 SimHash 签名分成4块后分别进行索引，提高检索的效率。

以64位的签名来说，把它以每16位划分块，共4块。 如果两个签名海明距离小于等于3，则至少有一个16位块完全相同。 但是我们不知道具体是哪两个块相同，所以要进行枚举，这里只需要枚举4次。

图 1.4.2 SimHash 签名分捅检索的过程

1. 当文本内容较长时，使用 SimHash 准确率很高，SimHash 处理短文本内容准确率往往不能得到保证；

2. 文本内容中每个term对应的权重如何确定要根据实际的项目需求，一般是可以使用IDF权重来进行计算。

1.4.4. KSentence算法

KSentence 算法基于一个朴素的假设：两个重复文本中，最长的K个句子应该是完全一样的。

算法步骤:

1. 预处理：读取文档数据集，根据需求，对文档中的中英文、简繁体等字符进行清洗和整理。

2. 提取语句：根据标点、换行符等划分语句，统计语句长度

3. 计算指纹：拼接最长的 \(K\) 个语句，计算 MD5 值作为文本指纹

4. 文本去重：根据文本指纹，过滤重复文本

关于 KSentence 算法的几点注解如下：

1. KSentence 算法的假设很严格，实验结果显示，KSentence 算法准确率较高，召回率低于 Minhash 和 Simhash 。

2. 算法实现简单，计算效率高，很容易并行化。算法对于具有固定格式的模板类文档具有很好的辨识能力，但对于抄袭后进行部分修改的文本识别度较低。

1.5. 话术去重