10. 最大后验估计

我们已经讲过概率模型的推断一般包括三类问题：条件概率查询、边缘概率查询和最大后验概率。 其中条件概率查询和边缘概率查询在计算上可以看成是等价的，可以运用消元法或者和积算法进行推断。 本周我们讨论模型推断中另一类问题：最大后验估计(maximum a posterior estimate,MAP)。

给定一个联合概率分布 \(p(\mathbf{x})=p(\mathrm{x}_1,\ldots,\mathrm{x}_N)\) ，我们把其中的变量分成两组，分别用E和F表示，其中E组表示证据变量(观测变量)，其值为固定值 \(\bar{x}_E\) 。 条件概率 \(p(x_F|\bar{x}_E)\) 又可以称之为后验概率，寓意是在有了观测(证据)数据 \(\bar{x}_E\) 之后 \(\mathrm{x}_F=x_F\) 的概率 ，所以称之为后验概率。

根据前面章节讨论的模型推断算法（消元法、和积算法）我们可以计算出条件概率 \(p(x_F|\bar{x}_E)\) 。

(10.4)\[p(x_F|\bar{x}_E) \propto p(x_F,\bar{x}_E) \triangleq \sum_{x_E} p(x_F,x_E)\delta(x_E,\bar{x}_E)\]

然而现在我们不再需要计算出某个具体的条件概率 \(p(x_F|\bar{x}_E)\) ， 而是希望得到这个条件概率分布中最大的概率 \(\max_{x_F}\ p(x_F|\bar{x}_E)\) ， 或者在取得最大概率时变量 \(x_F\) 的状态，即变量 \(x_F\) 是什么值时可以令这个条件概率（后验概率）取得最大值。 这个后验概率的最大值 \(\max_{x_F} p(x_F|\bar{x}_E)\) 称为 最大后验概率(maximum a posterior probability) ， 估计出极大值时变量的状态 称为最大后验估计(maximum a posterior estimate,MAP) 。

(10.5)\[x^{MAP}_{F}=\mathop{\arg \max}_{x_F} p(x_F|\bar{x}_E)\]

因为后验概率就是个条件概率而已，所以最大后验概率本质上就是最大条件概率。同样的，通过引入证据势函数， 可以把条件概率和边缘(联合)概率看成等价的，最大后验概率也可以看成最大边缘(联合）概率。 所以这里我们直接讨论极大化联合（也可以是边缘）概率，只需要在这基础上引入证据势函数就可以直接变成极大化后验(条件）。

(10.6)\[ \begin{align}\begin{aligned}\max_{x_F}\ p(x_F|\bar{x}_E) &\propto max_{x_F} \ p(x_F,\bar{x}_E)\\&= \max_{x_F} \ p(x_F,x_E)\delta(x_E,\bar{x}_E)\\&= \max_{\mathbf{x}} \ p(\mathbf{x})\delta(x_E,\bar{x}_E)\\&\triangleq \max_{\mathbf{x}} \ p^E(\mathbf{x})\end{aligned}\end{align} \]

备注

如果对于公式中的符号 \(\delta,E,\bar{x}_E\) 不理解请回顾一下 节 8.2.2 。

多数情况下，在最大后验估计中我们感兴趣的不是最大的后验概率值，而是取得最大后验概率时变量的状态。 这里我们先讨论如何计算最大概率值，然后再讨论如何在这基础上追溯出变量的状态。

10.1. 最大后验概率

这里我们先忽略证据(观测)变量E的存在，直接讨论如果获得一个联合概率的最大化的方法，然后可以通过非常简单的操作引入E。 那么我们要求一个联合(边缘)概率的最大值 \(\max_{\mathbf{x}} \ p(\mathbf{x})\) ， 是否可以分别独立求出其中每个变量的边缘概率 \(\max_{x_i} p(x_i)\) 的最大值，然后乘在一起呢？ 即 \(\max_{\mathbf{x}} \ p(\mathbf{x}) = \prod \max_{x_i} p(x_i)\) 。

我们通过一个具体的例子说明下，如 图 10.1.1 所示，有两个随机变量 \(\mathrm{x,y}\) ， 其边缘概率分布和条件概率分布用表格形式给出。 当 \(x=1\) 时，边缘概率 \(p(x)\) 取得最大值0.6，当 \(y=1\) 时，边缘概率 \(p(y)\) 取得最大值0.4， 按照最大边缘概率乘积的方法得到的联合概率为 \(p(x=1)p(y=1)=0.6\times0.4=0.24\) ， 然而实际上联合概率 \(p(x=1,y=1)=p(x=1)p(y=1|x=1)=0.6\times0=0\) ，这明显是不合理的。 所以，各个变量的边缘概率分别独立取得最大值，并不等价于它们的联合概率最大，除非这些变量是相互独立的。 可以思考一下，为什么变量是独立的时候就成立。

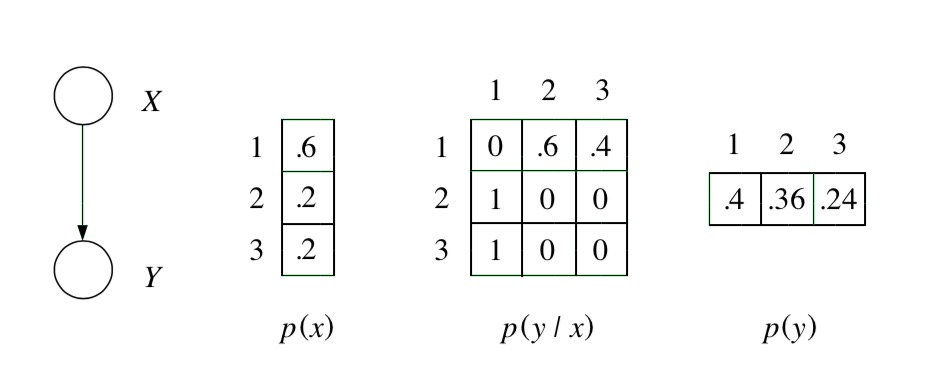
图 10.1.1 两个随机变量 \(\mathrm{x,y}\) 组成的概率分布。

我们从一个具体的例子来阐述如何求得一个联合概率分布的最大概率值。 如下图，是包含5个变量的无向图模型，我们假设图中变量都是伯努利变量，每个变量有两个取值 \(x_{i} \in\{0,1\}, \text { for } 1 \leq i \leq 5\) 。

我们把图中每条边上的势函数定义成 \(\psi_{i j}\left(x_{i}, x_{j}\right) = exp(\theta_{ij} x_i x_j)\) ，这个无向图的联合概率分布可以表示为：

(10.1.14)\[p(\mathbf{x}) = \frac{1}{Z} exp (\theta_{12} x_{1} x_{2} ) \cdot exp (\theta_{13} x_{1} x_{3}) \cdot exp(\theta_{24} x_{2} x_{4}) \cdot exp(\theta_{34} x_{3} x_{4}) \cdot exp(\theta_{35} x_{3} x_{5})\]

备注

不知道上述公式的含义？

在前面章节讲过，一个无向图联合概率分布可以写成定义在最大团的势函数的乘积。

(10.1.15)\[p_{\mathbf{x}}(\mathbf{x})=\frac{1}{Z} \prod_{(i, j) \in \mathcal{E}} \psi_{i j}\left(x_{i}, x_{j}\right)\]

其中Z是归一化系数，也叫配分函数，其实就是分子所有可能取值的求和，确保对于每个分子取值得到的是一个概率值，所有可能取值加起来为1。 如果不显示的写Z，就可以把等号换成”正比于”符号，表示得到的值正比于分子。

(10.1.16)\[p_{\mathbf{x}}(\mathbf{x}) \propto \prod_{(i, j) \in \mathcal{E}} \psi_{i j}\left(x_{i}, x_{j}\right)\]

在这个例子中， 团上的势函数 \(\psi_{i j}\left(x_{i}, x_{j}\right)\) 被定义成一个指数函数:

(10.1.17)\[\psi_{i j}\left(x_{i}, x_{j}\right) = exp(\theta_{ij} x_i x_j)\]

指数的连乘可以改写成幂的求和，也就得到了上述例子的等式。

(10.1.18)\[p(\mathbf{x}) = \frac{1}{Z} \prod_{(i, j) \in \mathcal{E}} \exp (\theta_{ij} x_i x_j) = \frac{1}{Z} \exp \sum_{i,j \in \mathcal{E}} \theta_{ij} x_i x_j\]

在这个例子中，我们假设 \(\theta_{12}=\theta_{34}=\theta_{35}=1,\theta_{13}=\theta_{24}=-1\) ，带入到上式可得:

(10.1.19)\[ \begin{align}\begin{aligned} p(\mathbf{x}) &= \frac{1}{Z} \exp (x_{1} x_{2}) \cdot exp(-x_{1} x_{3}) \cdot exp(-x_{2} x_{4}) \cdot exp(x_{3} x_{4}) \cdot exp(x_{3} x_{5})\\ &\propto \exp (x_{1} x_{2}) \cdot exp(-x_{1} x_{3}) \cdot exp(-x_{2} x_{4}) \cdot exp(x_{3} x_{4}) \cdot exp(x_{3} x_{5})\end{aligned}\end{align} \]

我们假设 \(\mathrm{x}_2,\mathrm{x}_3\) 是证据(观测)变量，即 \(\mathrm{x}_E=\{\mathrm{x}_2,\mathrm{x}_3\},E=\{2,3\}\) ， 并且观测值为 \(\{x_2=0,x_3=1\}\) 。 查询变量集合为 \(\mathrm{x}_F=\{\mathrm{x}_1,\mathrm{x}_4,\mathrm{x}_5\}\) ， 现在我们的目标是计算出后验概率 \(p(\mathrm{x}_F|\mathrm{x}_E)\) 的最大概率值:

(10.1.20)\[ \begin{align}\begin{aligned}\max_{\mathrm{x}_F} p(\mathrm{x}_F|\mathrm{x}_E) & \propto \max_{\mathbf{x}} p(\mathrm{x}_F,\mathrm{x}_E) \delta(\mathrm{x}_E,\bar{x}_E)\\&= \max_{x_1,x_2,x_3,x_4,x_5} p(x_1,x_2,x_3,x_4,x_5)\delta(x_2,0)\delta(x_3,1)\\& \propto \max_{x_1,x_2,x_3,x_4,x_5} \exp (x_{1} x_{2}) \cdot exp(-x_{1} x_{3}) \cdot exp(-x_{2} x_{4}) \cdot exp(x_{3} x_{4}) \cdot exp(x_{3} x_{5}) \delta(x_2,0)\delta(x_3,1)\\ &= \max_{x_1} \max_{x_2} \max_{x_3} \max_{x_4} \max_{x_5} \exp (x_{1} x_{2}) \cdot exp(-x_{1} x_{3}) \cdot exp(-x_{2} x_{4}) \cdot exp(x_{3} x_{4}) \cdot exp(x_{3} x_{5}) \delta(x_2,0)\delta(x_3,1)\end{aligned}\end{align} \]

仔细观察下 公式(10.1.20) ，发现其和消元法的公式非常类似，如果要对这个无向图模型进行消元法，假设消元顺序是(5,4,3,2,1)， 那么消元法的公式为：

(10.1.21)\[ \begin{align}\begin{aligned}1 &= \frac{1}{Z} \sum_{x_1} \sum_{x_2} \sum_{x_3} \sum_{x_4} \sum_{x_5} \exp (x_{1} x_{2}) exp(-x_{1} x_{3}) exp(-x_{2} x_{4}) exp(x_{3} x_{4}) exp(x_{3} x_{5}) \delta(x_2,0)\delta(x_3,1)\\&= \frac{1}{Z} \sum_{x_1} \sum_{x_2} \exp (x_{1} x_{2}) \delta(x_2,0) \sum_{x_3} exp(-x_{1} x_{3}) \delta(x_3,1) \sum_{x_4} exp(-x_{2} x_{4}) exp(x_{3} x_{4}) \sum_{x_5} exp(x_{3} x_{5})\end{aligned}\end{align} \]

因为我们把模型中所有结点都消除了，所以最后结果是1。1的问题不是重点，重点是在这个公式中求和符号是满足交换和结合律的， 所以这些求和符号可以从最外面移到内侧对应位置，事实上，\(\max\) 操作符也符合这样的性质，所以也可以像求和符号一样移到内部， 这里我们省略证明，有兴趣的读者可以自己查找”交换半环(commutative semiring)”相关理论。 对 公式(10.1.20) 进行类似处理可得到和消元法类似的结构。

(10.1.22)\[\max_{\mathbf{x}} p(\mathrm{x}_F,\mathrm{x}_E) \delta(\mathrm{x}_E,\bar{x}_E) \propto \max_{x_1} \max_{x_2} \exp (x_{1} x_{2}) \delta(x_2,0) \max_{x_3} exp(-x_{1} x_{3})\delta(x_3,1) \max_{x_4} exp(-x_{2} x_{4}) \cdot exp(x_{3} x_{4}) \max_{x_5} exp(x_{3} x_{5})\]

类似消元法的过程，我们把包含 \(x_5\) 的部分 \(\max_{x_5} exp(x_{3} x_{5})\) 组在一起 \(m_{5}\left(x_{3}\right)\) 。

• 当 \(x_3=1\) 时， \(x_5\) 选取1， \(m_5\) 是最大；

• 当 \(x_3=0\) 时， \(x_5\) 选取1或0 ， \(m_5\) 都是最大。

这时可以看出，对于 \(x_3\) 的所有可能取值，当 \(x_5=1\) 时，这一部分取得最大值，所以:

(10.1.23)\[m_{5}\left(x_{3}\right)=\max _{x_{5}} \exp \left(x_{3} x_{5}\right) = \exp(x_{3})\]

这个过程非常类似于消元法，消元法是通过求和进行变量消除，但是这里求和符号变成了max，把求和改成选取一个最大值。 我们用表格的形式表示 \(m_5(x_3)\) 的值。 对于 \(m_5(x_3=0)\) ，选取 \(x_5=1\) 能令 \(m_5(x_3=0)\) 取得最大值； 对于 \(m_5(x_3=1)\) ，选取 \(x_5=1\) 能令 \(m_5(x_3=1)\) 取得最大值。

(10.1.24)\[\begin{split}m_5(x_3) = \begin{array}{|c|c|c|} \hline x_3& x_5&m_5 \\\hline 0&0&\exp(0) \\\hline 0&1&\exp(0) \\\hline 1&0&\exp(0) \\\hline 1&1&\exp(1) \\\hline \end{array} \mathop{\Longrightarrow}^{\max_{x_5}} \begin{array}{|c|c|c|} \hline x_3& max_{x_5} & m_5 \\\hline 0&0 or 1 &\exp(0) \\\hline 1&1&\exp(1) \\\hline \end{array} = \begin{array}{|c|c|c|c|} \hline x_3& m_5(x_3) \\\hline 0& \exp(0) \\\hline 1& \exp(1) \\\hline \end{array}\end{split}\]

接下来我们需要计算 \(m_4(x_2,x_3)\) ：

(10.1.25)\[ \begin{align}\begin{aligned}m_4(x_2,x_3) &= \max_{x_4} exp(-x_{2} x_{4}) \cdot exp(x_{3} x_{4}) m_{5}\left(x_{3}\right)\\&= \max_{x_4} exp(-x_{2} x_{4}) \cdot exp(x_{3} x_{4}) \cdot \exp(x_{3})\\&= \max_{x_4} exp(-x_{2} x_{4} + x_{3} x_{4} + x_{3})\end{aligned}\end{align} \]

\(m_4\) 是一个关于 \(x_2,x_3\) 的函数，通过”消除” \(x_4\) 使得 \(m_4\) 在任意 \(x_2,x_3\) 的情况下都能取得对应情况下的最大值， 我们同样用表格的形式来展示这个过程。这个表格展示的时在 \(x_2,x_3\) 取不同值时(分布表)，\(x_4\) 需要为什么值才能领 \(m_4\) 最大，以及这个最大是又是什么。

(10.1.26)\[\begin{split}m_4(x_2,x_3) = \begin{array}{|c|c|c|c|} \hline x_2&x_3& x_4 & m_4 \\\hline 0&0& 0 & \exp(0) \\\hline 0&0& 1 & \exp(0) \\\hline 0&1&0 & \exp(1) \\\hline 0&1&1 & \exp(2) \\\hline 1&0&0 & \exp(0) \\\hline 1&0&1 & \exp(-1) \\\hline 1&1& 0 & \exp(1) \\\hline 1&1& 1 & \exp(1) \\\hline \end{array} \mathop{\Longrightarrow}^{\max_{x_4}} \begin{array}{|c|c|c|c|} \hline x_2&x_3& \max_{x_4} & m_4(x_2,x_3) \\\hline 0&0& 0 or 1 & \exp(0) \\\hline 0&1&1 & \exp(2) \\\hline 1&0&0 & \exp(0) \\\hline 1&1& 0or1 & \exp(1) \\\hline \end{array}\end{split}\]

回想一下，在边缘概率推断的消元法中，是通过对 \(x_4\) 求和进行消除，即 \(m_4(x_2=0,x_3=0) = \sum_{x_4} m(x_2=0,x_3=0,x_4)\) 。 而在这里是通过选取一个最大的方法消除 \(x_4\) ， \(m_4(x_2=0,x_3=0)=\mathop{max}_{x_4} m(x_2=0,x_3=0,x_4)=m(x_2=0,x_3=0,x_4=1)\) 。 得到 \(m_4\) 之后，下一步需要计算 \(m_3\) ：

(10.1.27)\[m_3(x_1,x_2) = \max_{x_3} exp(-x_1 x_3) \delta(x_3,1) m_4(x_2,x_3)\]

这一步我们需要消除 \(x_3\) ，并且令 \(m_3\) 分布表中每种可能(每行)都是最大值。 我们把上面 \(m_4\) 的表格结果代入到 \(exp(-x_1 x_3) m_4(x_2,x_3) \delta(x_3,1)\) 得到的所有可能取值形成的表格， 然后通过选取合适的 \(x_3\) 的值（同时消除掉了 \(x_3\) ）使得 \(m_3(x_1,x_2)\) 极大化。 然而注意到变量 \(\mathrm{x}_3\) 是证据变量，并且其观测是1。 比如对于 \(m_3(x_1=0,x_2=0)\) ：

• 当 \(x_3=0\) 时， \(\delta(x_3,1)=0 \rightarrow m_3(x_1=0,x_2=0)=0\)

• 当 \(x_3=1\) 时， \(\delta(x_3,1)=1 \rightarrow m_3(x_1=0,x_2=0)=exp(2)\)

所以选取 \(x_3=1\) 可以使得 \(m_3(x_1=1,x_2=0)\) 取得最大。

(10.1.28)\[\begin{split}m_3(x_1,x_2) = \begin{array}{|c|c|c|c|c|}\hline x_1&x_2&x_3 & m_4(x_2,x_3)&m_3(x_1,x_2) \\\hline 0&0&0& \exp(0) & 0 \\\hline 1&0&0& \exp(0)& 0 \\\hline 0&0&1 & \exp(2)& \exp(2) \\\hline 1&0&1 & \exp(2)& \exp(1) \\\hline 0&1&0 & \exp(0) & 0 \\\hline 1&1&0 & \exp(0) & 0 \\\hline 0&1&1 & \exp(1)& \exp(1) \\\hline 1&1&1 & \exp(1)& \exp(0) \\\hline \end{array} \mathop{\Longrightarrow}^{\max_{x_3}} \begin{array}{|c|c|c|c|}\hline x_1&x_2& \max_{x_3} &m_3(x_1,x_2) \\\hline 0&0&1 & \exp(2) \\\hline 1&0&1 & \exp(1) \\\hline 0&1&1 & \exp(1) \\\hline 1&1&1 & \exp(0) \\\hline \end{array} = \begin{array}{|c|c|c|}\hline x_1&x_2 &m_3(x_1,x_2) \\\hline 0&0 & \exp(2) \\\hline 1&0 & \exp(1) \\\hline 0&1 & \exp(1) \\\hline 1&1 & \exp(0) \\\hline \end{array}\end{split}\]

到这一步 公式(10.1.22) 就变成了：

(10.1.29)\[\max_{\mathbf{x}} p(\mathrm{x}_F,\mathrm{x}_E) \delta(\mathrm{x}_E,\bar{x}_E) \propto \max_{x_1} \max_{x_2} \exp (x_{1} x_{2}) \delta(x_2,0) m_3(x_1,x_2)\]

接下来，我们定义 \(m_2(x_1)=\max_{x_2} \exp (x_{1} x_{2}) \delta(x_2,0) m_3(x_1,x_2)\) ，代入 \(m_3(x_1,x_2)\) 的表格结果，计算出 \(m_2(x_1)\) 。

(10.1.30)\[\begin{split}m_2(x_1)= \begin{array}{|c|c|c|c|}\hline x_1&x_2 &m_3(x_1,x_2)&m_2(x_1) \\\hline 0&0 & \exp(2)& exp(2) \\\hline 1&0 & \exp(1)& exp(1) \\\hline 0&1 & \exp(1)& 0 \\\hline 1&1 & \exp(0)& 0 \\\hline \end{array} \mathop{\Longrightarrow}^{\max_{x_2}} \begin{array}{|c|c|c|}\hline x_1& \max_{x_2} &m_2(x_1) \\\hline 0& 0 & exp(2) \\\hline 1& 0 & exp(1) \\\hline \end{array} = \begin{array}{|c|c|c|}\hline x_1 &m_2(x_1) \\\hline 0& exp(2) \\\hline 1& exp(1) \\\hline \end{array}\end{split}\]

最后，可以看出当 \(x_1=0\) 的时候可以取得最大值。

(10.1.31)\[ \begin{align}\begin{aligned}\max_{\mathrm{x}_F} p(\mathrm{x}_F|\mathrm{x}_E) &= \max_{\mathbf{x}} \frac{1}{z} p(\mathrm{x}_F,\mathrm{x}_E) \delta(\mathrm{x}_E,\bar{x}_E)\\&= \max_{x_1} \frac{1}{z} m_2(x_1)\\&= \frac{m_2(x_1=0)}{m_2(x_1=0)+m_2(x_1=0)}\\&= \frac{exp(2)}{exp(2)+exp(1)}\end{aligned}\end{align} \]

我们可以把最大后验概率的算法看做是消元法的一个”变形” ，消元法是计算出 后验概率分布 ，而最大后验概率是计算出 后验概率最大值 。 同理，我们把和积算法中的sum改成max，就可以使用和积算法的”变形”计算出最大后验概率。

提示

熟悉动态规划的读者可以发现最大后验概率的计算过程实际上是动态规划的过程，但这里我们没有从动态规划的角度去阐述最大后验概率算法， 而是从消元法变形的角度去阐述，是为了能让读者和消元法进行对比，能更容易”记住”这个算法过程，动态规划实在是太难以理解了。

10.2. 最大化后验的状态

在大多数情况下，我们需要的不是后验概率的最大值，而是当后验概率分布取得最大值时变量的状态(即变量的取值)。 所以最大后验估计指的是后验概率分布取得最大值时变量的状态。

(10.2.14)\[x_{F}^{MAP} \in \mathop{\arg \max}_{\mathrm{x}_F} p(\mathrm{x}_F|\bar{x}_E)\]

要想获得在后验概率取得最大值时，查询变量 \(\mathrm{x}_F\) 的状态值，就需要在计算最大后验概率的过程中 我们记录下每一步max时被”消除”变量的状态值，在执行完最大后验概率计算后，我们再回溯回去。

比如上面的例子中，我们消元顺序是(5,4,3,2,1)，那么在计算完最大后验概率后，我们反序回溯。 最后一个被消除的变量是 \(\mathrm{x}_1\) ，并且是 \(x_1=0\) 时取得最大值，回溯出来 \(x_1=0\) ；

然后是变量 \(\mathrm{x}_2\) ，我们已经确认 \(x_1=0\) ，所以回溯的路径是 \(x_1=0\) 的路径， 在 \(x_1=0\) 的路径上，我们是选取了 \(x_2=0\) 使得 \(m_2(x_1)\) 达到最大值，所以回溯出 \(x_2=0\) 。

接下来回溯变量 \(\mathrm{x}_3\) ，在 \(x_1=0,x_2=0\) 的路径上，我们是选取了 \(x_3=1\) 使得 \(m_3(x_1,x_2)\) 达到最大值，所以回溯出 \(x_3=1\) 。

接下来回溯变量 \(\mathrm{x}_4\) ，在 \(x_2=0,x_3=1\) 的路径上，我们是选取了 \(x_4=1\) 使得 \(m_4(x_2,x_3)\) 达到最大值，所以回溯出 \(x_4=1\) 。

接下来回溯变量 \(\mathrm{x}_5\) ，在 \(x_3=1\) 的路径上，我们是选取了 \(x_5=1\) 使得 \(m_5(x_3)\) 达到最大值，所以回溯出 \(x_5=1\) 。

所以我们得到最大后验估计：

(10.2.15)\[x_1=0,x_2=0,x_3=1,x_4=1,x_5=1\]

在回溯过程中，我们发现有些路径上某些变量的值不是唯一的，也就是某些变量无论取值0或1都能使得最终的概率值取得极大值， 所以 最大后验估计可能有多个解 。

10.3. 本章总结