2. Attention&Transformer&Bert 简介

Transformer 模型是2017年谷歌发表的论文《attention is all you need》中提出的 seq2seq 模型， 它是一个基于神经网络的模型，它的输入可以是一个序列，输出是另一个序列。 而 attention 是 Transformer 模型中用于提取特征的一种算法或者机制，可以把它看做是神经网络中的一个层。

BERT 是由谷歌提出的一种预训练模型解决方案，来源于谷歌的一篇论文。 《BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding》 (https://arxiv.org/abs/1810.04805) 翻译过来就是”预训练的深层双向 Transformer 语言模型”。 Bert 并不是一个具体的算法，直白的讲，它就是一个预训练好 Transformer， 这个预训练好的模型（参数）可以应用于各类NLP任务，比如文本分类、翻译、标注等等。

本文基本是翻译自博客 ：The Illustrated Transformer (https://jalammar.github.io/illustrated-transformer/)。 英语阅读无障碍的同学可以直接阅读英文博客。

2.1. Transformer 从宏观到微观

2.1.1. seq2seq

图 2.1.6 图片来源：https://jalammar.github.io/illustrated-transformer/

首先，Transformer 就是一个 seq2seq 的模型，它的输入可以是一个序列，输出是另一个序列。 输入序列可以是一段文本，输出序列可以是另一种语言对应的文本，这样就可以用来做翻译。 此外，模型对输入序列的长度并没有特别限制，输入和输出序列的长度也可以不一样。

输入和输出序列并不是必须是文本序列，任意序列数据都是可以的，比如用户的点击行为序列。

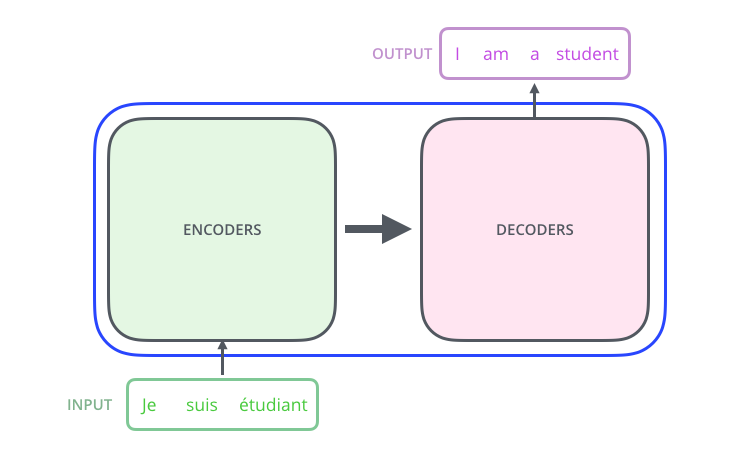
图 2.1.7 图片来源：https://jalammar.github.io/illustrated-transformer/

Transformer 内部可以拆成两个单元，一个是编码(encoder)单元，一个是解码（decoder）单元。 编码单元负责抽取输入序列的特征，解码单元负责把编码特征解码成输出序列

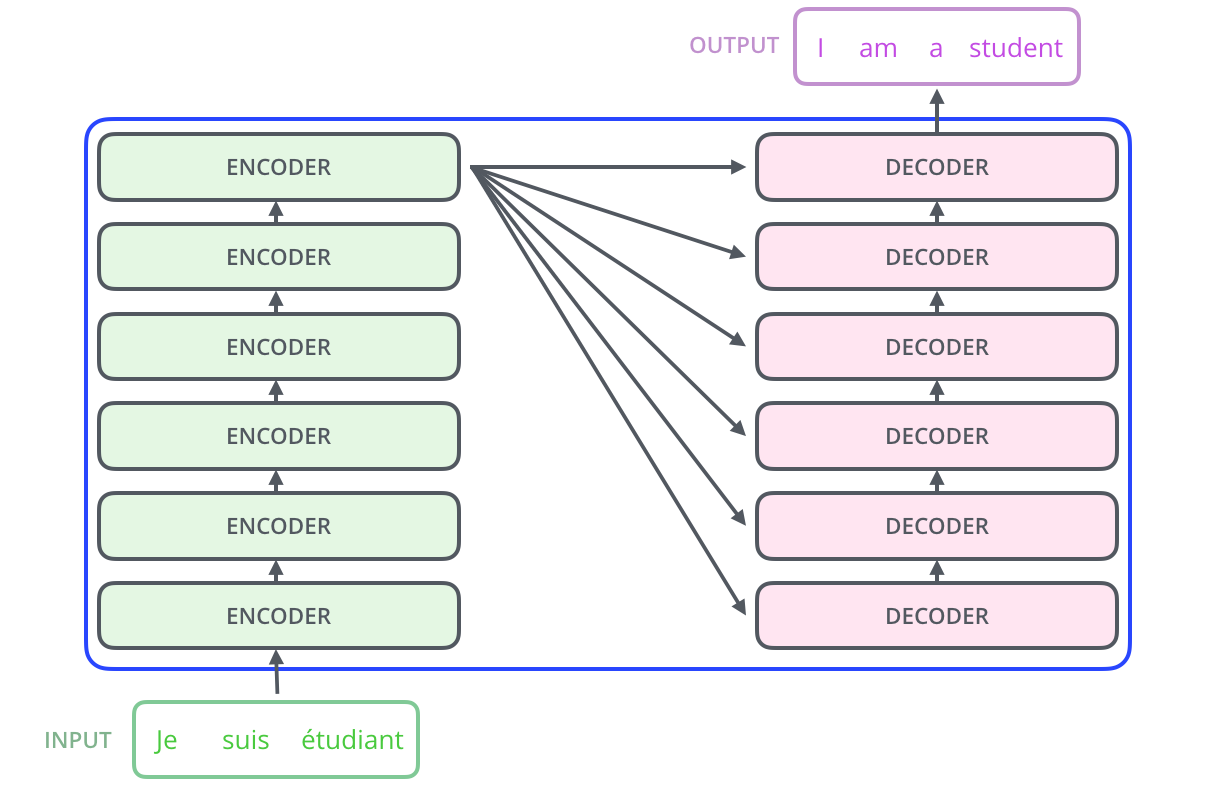
图 2.1.8 图片来源：https://jalammar.github.io/illustrated-transformer/

无论是编码单元，还是解码单元，其内部都是一个重复的堆叠结构。 编码单元是编码层（encoder layer）的重复堆叠，每一层都是完全一样的结构。 同理，解码单元是解码层（decoder layer）的重复堆叠。 重复堆叠的次数并没有固定的限制，但层数越多，模型就越复杂（参数越多），好处是模型表达能力变强， 缺点是模型（计算）性能下降，需要的训练数据也更多，模型的训练和推理时间都变长。

图 2.1.9 图片来源：https://jalammar.github.io/illustrated-transformer/

编码层（encoder layer）内部又分为两层，Self-Attention 层和前馈网络层（FFNN）， 有关 Self-Attention 的细节我们下一节再讨论， 前馈网络层（FFNN）就是简单的全连接层。

图 2.1.10 图片来源：https://jalammar.github.io/illustrated-transformer/

解码层内部也是类似的结构，不过它比编码层多了一个特殊的层（Encode-Decoder Attention）， 我们暂时先不用管它。

2.1.2. 模型的输入

我们知道计算机只能处理数值数据，计算机是无法直接处理人类语言符号的，我们需要把语言符号转成数值类型数据。

Token

习惯上，我们把序列中的元素称为 token，比如英语文本序列中每个英文单词是一个 token； 中文文本序列中每个汉字是一个 token。token 是序列处理中的逻辑最小单元，根据对序列的处理方法进行定义。 比如，对于中文文本序列，如果想按照组成序列的词组进行处理，那分词后的每个词组就是一个 token。

在机器学习算法中，经常需要处理各类符号（非数值）数据，需要把符号数据转存数值数据后再喂给模型。 转化方法比较简单，常用的方法就是 OneHot， 即给每个符号分配一个唯一的整数编号，整数编号和符号一一对应。 OneHot 方法简单粗暴，易理解。 但缺点也很明显，一方面不能表达任何与符号相关的信息，另一方面转换后的向量（矩阵）非常稀疏。

之后在 OneHot 的基础上发展出另一个方法，把每个 token 映射到一个稠密的向量上， 向量的长度可以任意设置，这种方法称为嵌入法（embedding）， 映射成的向量称为嵌入向量（embedding vector）, 所有 token 的嵌入向量组成的空间称为嵌入空间。

当然，每个 token 的嵌入向量的值是需要从数据中学习得到的，学习的方法有很多，比如 word2vec、glove、Elmo等等，以及我们今天讨论的 BERT。

Transformer 的输入层就是把每个 token 先映射到一个嵌入向量(embedding vector)， 把 token 变成一个嵌入向量的序列后，再传递给编码层。

图 2.1.11 图片来源：https://jalammar.github.io/illustrated-transformer/

图 2.1.12 图片来源：https://jalammar.github.io/illustrated-transformer/

这里一个关键的特点是，序列中的 token 是独立输入到模型的，

2.2. Self-Attention

2.2.1. 什么是注意力？

假设我们要翻译如下的英文句子

”The animal didn't cross the street because it was too tired。"

句子中代词 it 指代的是什么呢？是 “animal” 还是 “street”？ 对于人来说，可以很容易给出答案，然而对于机器（模型）来说，这并不容易。

如何让模型知道序列中的 “it” 是和 “animal” 相关的？换句话说， 序列中的token并不是孤立的，互相之间是存在某些关联的，而这种联系对于整个序列来说是至关重要的。 如果你熟悉 RNN 系列的模型，你知道它是通过隐状态来记录序列前面的信息的。 Attention 是 Transformer 中用于学习 token 之间关联关系的机制。

图 2.2.3 图片来源：https://jalammar.github.io/illustrated-transformer/

一言以蔽之，Attention 就是用来衡量一个序列中 token 之间的关联关系及其强弱的。 注意，不要崇拜它，Attention 不是什么神迹，它的能力其实并不强。 其实它对 token 之间关系的表达能力是比较弱的。

2.2.2. 加权求和

Attention 并不复杂，事实上还很简单，复杂程度和树模型、SVM相比差远了， 所以请不要恐慌。

图 2.2.4 图片来源：https://jalammar.github.io/illustrated-transformer/

编码层输入的是 token 对应的嵌入向量序列，输出也是每个token一个向量， 输入和输出按照 token 是一一对应的，每个 token 有一个输入也有一个输出。 核心问题就是：如何得到每个token的输出向量？ 还要考虑到 token 之间的关联性，不能孤立的计算每个 token 的输出， 而要想办法 “引入” 序列中其它 token 的信息。

解决方法很简单：加权求和！ 下一步就是，权重怎么来？求谁的和？

首先，我们为 每个 token 分别设定 三个（长度相同）特殊的向量：

• Query ： 查询向量

• Key：

• Value：值向量，表达 token 的信息

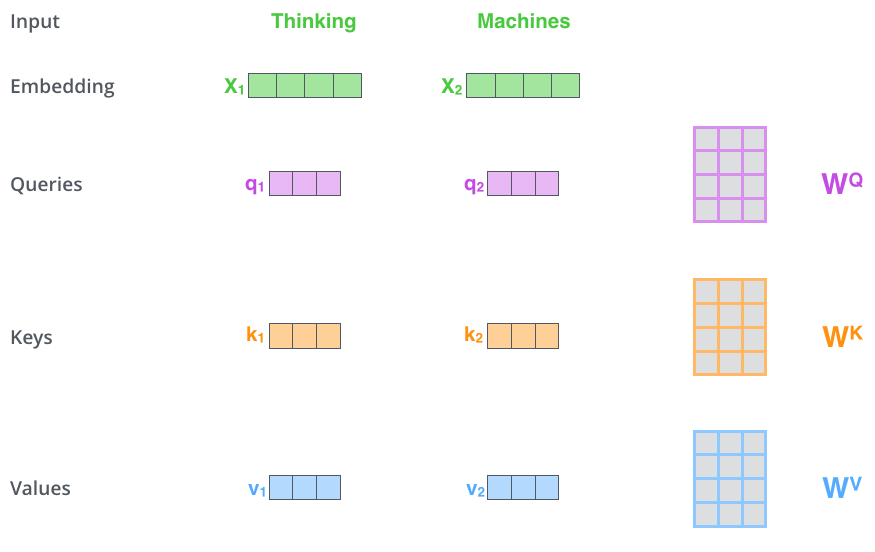
符号 \(x_i\) 表示 Self-Attention 层的第 \(i\) 个 token 的输入向量， Self-Attention 层内部存在三个矩阵， 分别是 \(W^Q,W^K,W^V\)。

假设 \(x_i\) 的尺寸是 \(1\times N\)， \(W^Q,W^K,W^V\) 三个矩阵的尺寸就是 \(N \times P\)， 其中 \(P\) 的值是可以人为指定的，一般是 \(64\)。

对于第 \(i\) 个 token 来说，有

(2.2.65)\[ \begin{align}\begin{aligned}q_i = x_i \boldsymbol{\cdot} W^Q\\k_i = x_i \boldsymbol{\cdot} W^K\\v_i = x_i \boldsymbol{\cdot} W^V\end{aligned}\end{align} \]

第 \(i\) 个 token 的输出向量计算方法为：

1. 用 \(q_i\) 依次乘以（点积、內积）其它 token 的 key 向量，得到一系列的 score。

   (2.2.66)\[s_{ij} = q_i \boldsymbol{\cdot} k_j\]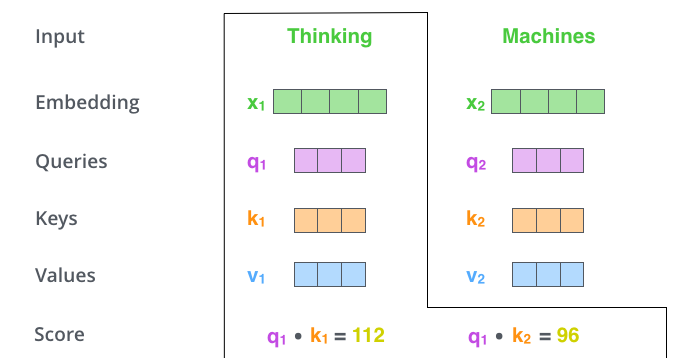

   

2. 把 \(s_{ij}\) 除以 \(\sqrt{d_k}\) 进行缩放， \(d_k\) 表示 Key 向量的长度。原因是 \(s_{ij}\) 是通过內积得到的， 內积的方差会受到向量长度的影响，除以 \(\sqrt{d_k}\) 相当于对內积的方差进行了控制，在反向传播时可以得到比较平稳的梯度。

3. 利用 \(\mathop{softmax}\) 对 \(s_{i*}\) 进行归一化，归一化后的结果就是权重值，一般称为注意力值（attention value）。 \(\mathop{softmax}\) 确保权重值为正并且和为 1 。

   (2.2.67)\[a_{ij} = \frac{ e^{s_{ij}} }{\sum e^{s_{ij}} }\]

   

4. 对所有 token 的 value 向量进行加权求和，得到当前第 \(i\) 个 token 的输出向量。

   (2.2.68)\[z_i = \sum_{j} a_{ij} v_j\]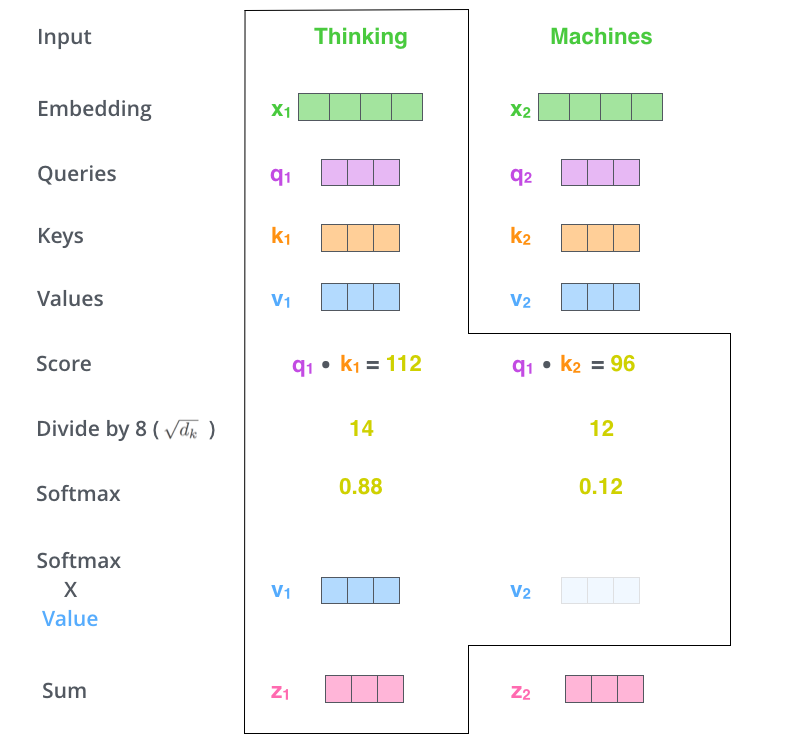

   

矩阵实现

上面我们是以单个 token 的视角对 Self-Attention 的过程进行描述的， 现在看下如果利用矩阵操作，对整个序列进行处理。

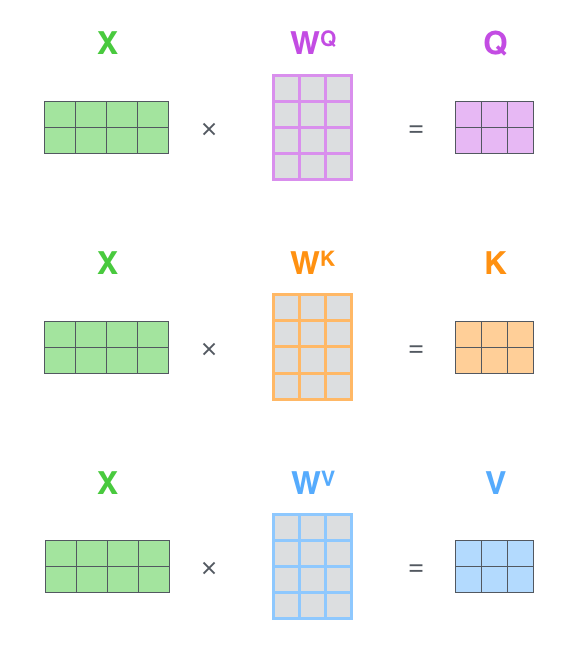
我们把输入的向量 \(x_i\) 序列，拼接成一个矩阵 \(X\) ， \(X\) 矩阵的第 \(i\) 行就是第 \(i\) 个 token 的输入向量 \(x_i\) 。得到 \(q、k、v\) 的过程完全可以通过矩阵实现。 最后的加权求和过程，也可以在矩阵上实现。

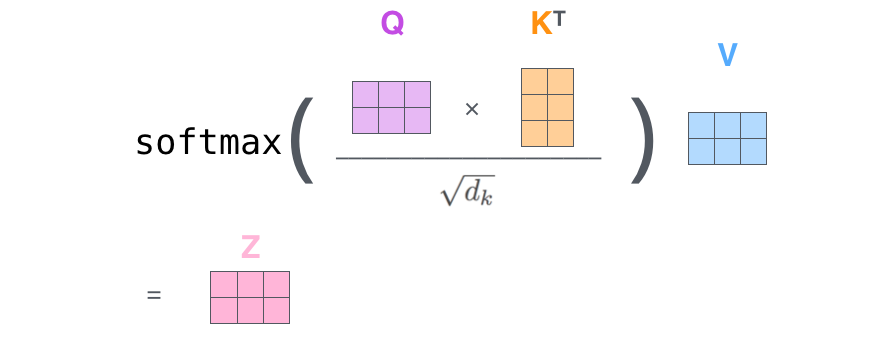
2.2.3. 位置编码

回顾一下整个过程，我们发现 Attention 机制没有考虑到 token 在序列中的位置， 序列中 token 的位置不影响最终的输出，这明显是不行的。

Transformer 的解决方法就是为每一个 \(x_i\) 加上编码了位置信息的常量向量。

(2.2.69)\[ \begin{align}\begin{aligned}x = x +position_enc(x)\\x \rightarrow encoding(x)\end{aligned}\end{align} \]

(2.2.70)\[ \begin{align}\begin{aligned}PE(pos,2i) = sin (pos / 10000^{2i/d_{model}})\\PE(pos,2i+1) = cos (pos / 10000^{2i/d_{model}})\end{aligned}\end{align} \]

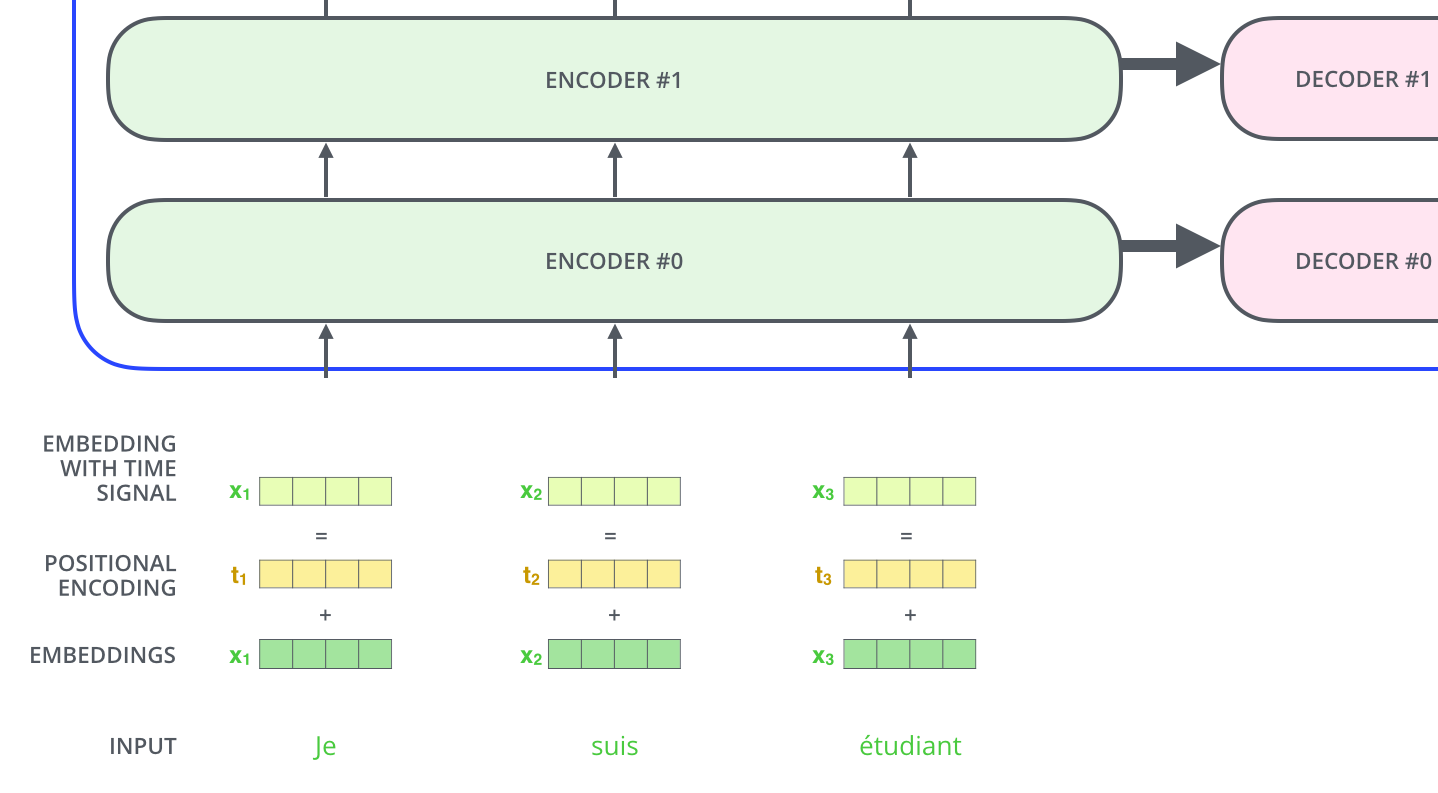
\(pos\) 表示 token 在序列中的位置，\(d_{model}\) 表示编码向量的长度（等于嵌入向量的长度）， \(i\) 表示编码向量中的位置。

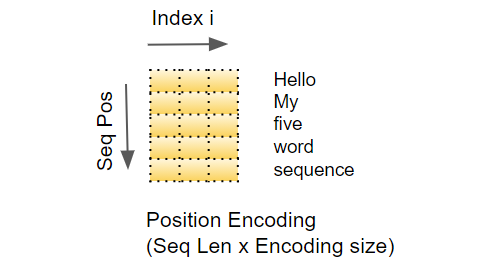
注意， \(position\ vector\) 是常量，不需要模型学习。 一个例子如下。

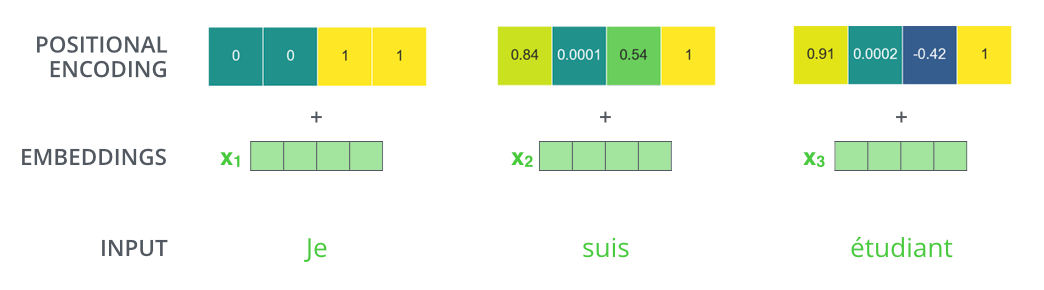
那么，这个位置编码到底是什么呢？

在下图中，第一行是一个位置的编码向量。 每行包含 512 个值——每个值都在 1 到 -1 之间。 我们对它们进行了颜色编码，使其更加直观。

我们需要知道的是，实现位置编码的方法并不唯一，这里的方法是论文 《Attention is all you need》 中的方法，除此之外也可以采用其它的方法。

2.2.4. 多头注意力（Multi-head）

明白了 Attention 机制后，就能发现所谓的 Attention 就是每个 token 在某个层面上可以与序列中其它 token 存在联系。 但 Attention 通过 softmax 归一化了权重， 这使得一个 token 和其它 token 的联系有了 强弱 限制， 注意力分数（attention score） 就是对这种联系的 强弱 度量。

然而，如果某个 token 和序列中的多个其它 token 存在 不同层面的不可比较 的联系怎么办？ 此时，可以平行计算多次 Attention 机制， 每一次 Attention 表示不同层面的表达。

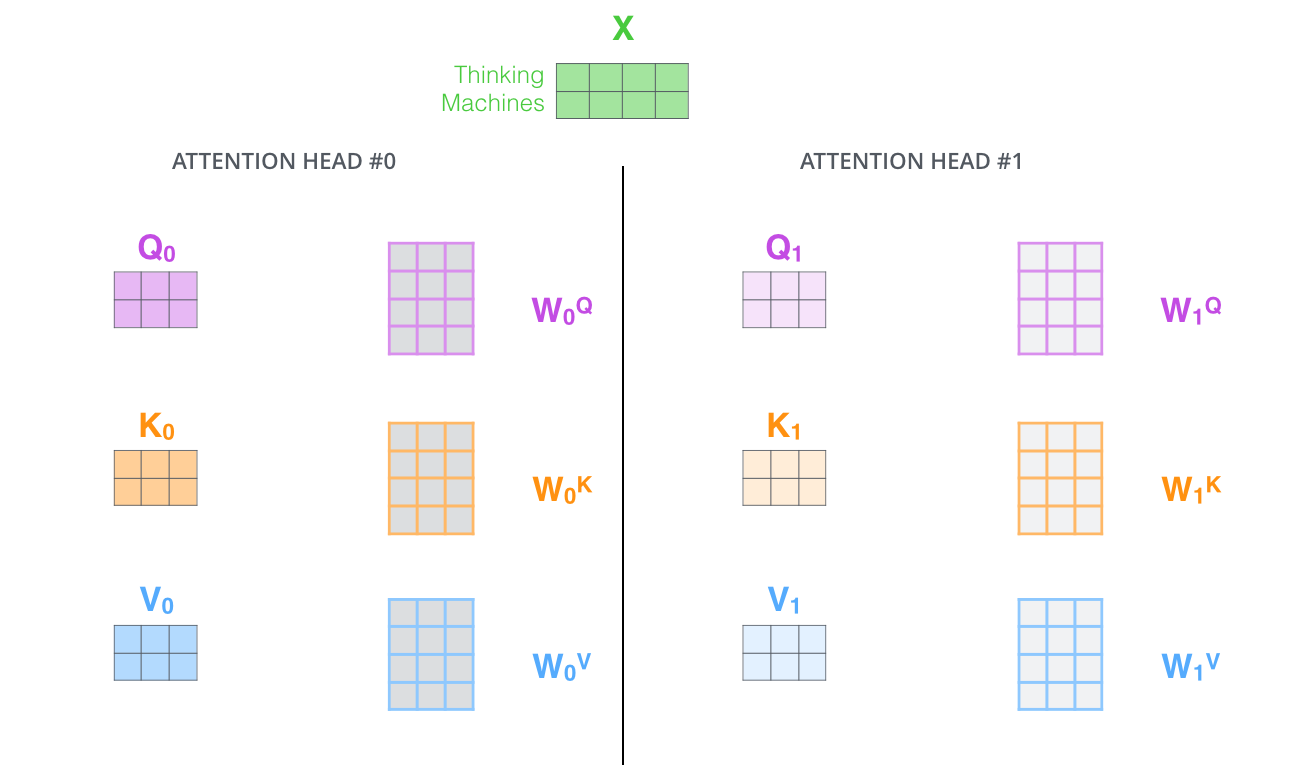
我们把一次 Attention 称为一个 head ， 多次 Attention 就称为多头机制(Multi-head)。 注意，在多头注意力中，各个 head 之间的参数（\(Q、K、V、W^Q、W^K、W^V\)）都是独立的。

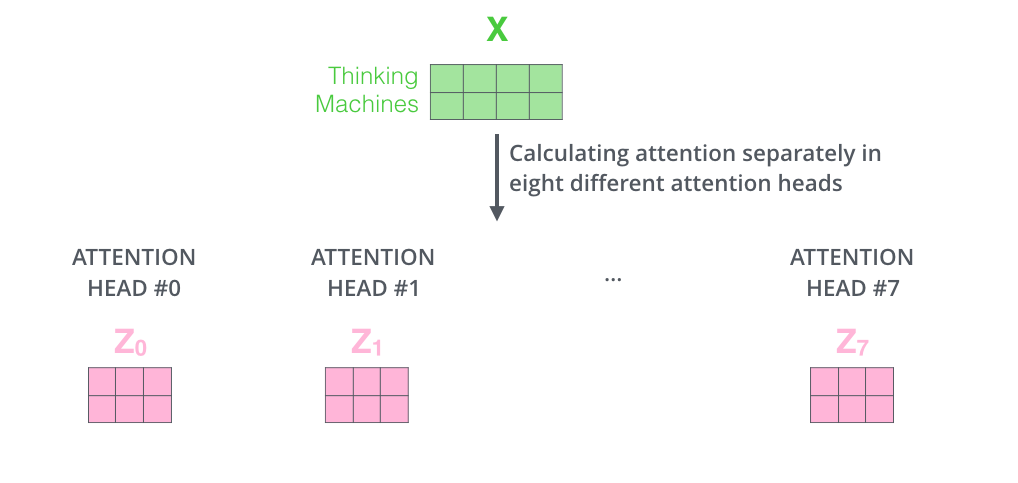
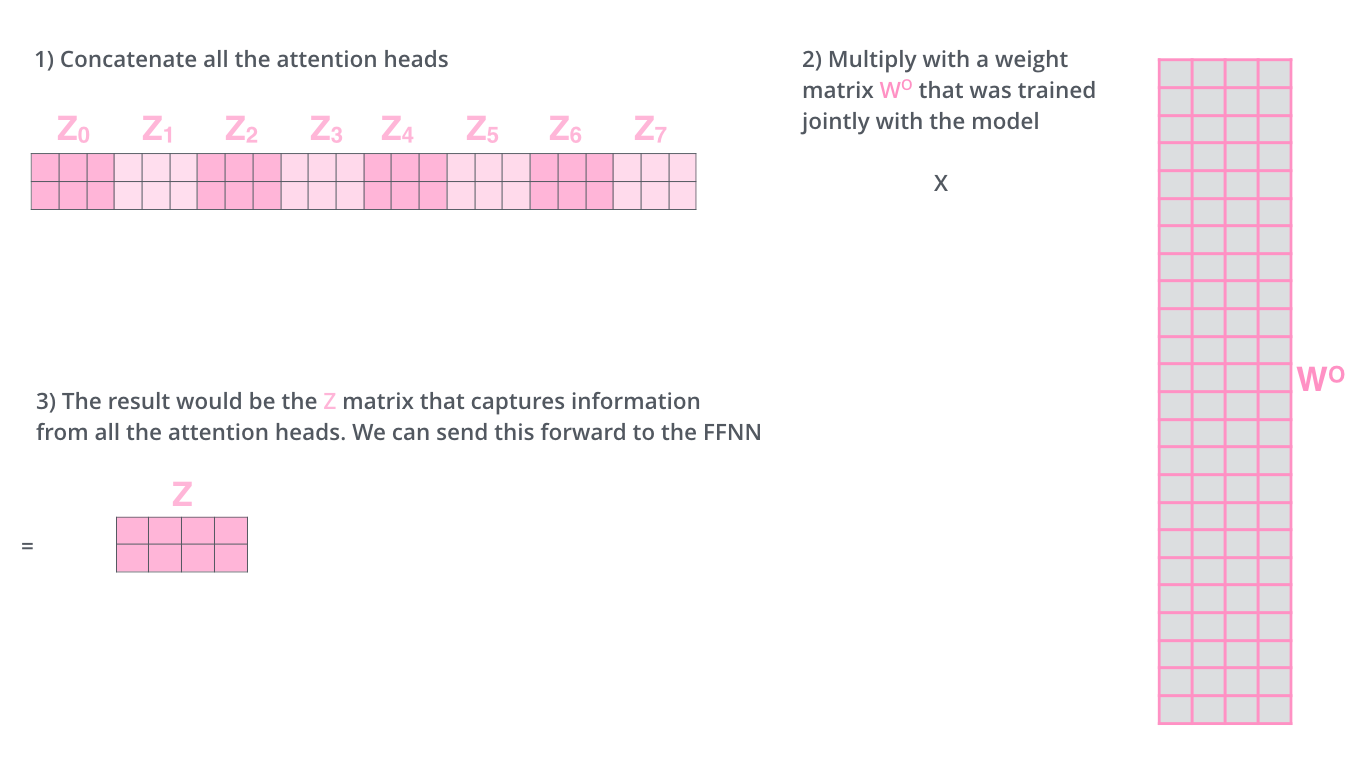
在 Transformer 中默认用的 \(8\) 头，每个头都会产生一个 \(Z\) 。 这里就需要把这多个 \(Z\) 合并成一个，合并的方法也比较简单。 先把多个 \(Z\) 拼接，然后通过一个权重矩阵映射。

2.3. Attention 机制

深度学习中的注意力可以广义地解释为重要性权重

2.4. 其它参考资料

[1]

The Illustrated Transformer

[2]

Transformer — Attention is all you need

[3]

Transformers Explained Visually (Part 1): Overview of Functionality

[4]

Transformers Explained Visually (Part 2): How it works, step-by-step

[5]

Transformers Explained Visually (Part 3): Multi-head Attention, deep dive

[6]

Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention)

[7]

Attention? Attention!

[8]

一篇了解NLP中的注意力机制

[9]

Transformers and Multi-Head Attention