15. 马尔科夫蒙特卡洛¶
对于难于精确推断的模型结构,我们可以近似推断(approximate inference), 近似推断的方法一般有两种:变分法(variational)和采样法(sample)。 其中,变分法并不能解决我们所面临的所有情况,这时我们就可以尝试使用抽样法解决。 理论上,只要有足够的样本我们就得到概率分布任意重要信息。
15.1. Why sampling?¶
给出服从概率分布 \(p_{\mathbf{x}}(\mathbf{x})\) 的N个样本 \(\left\{\mathbf{x}^{1}, \ldots, \mathbf{x}^{N}\right\}\) 。 我们可以求出样本的均值:
无论这N个样本是否是互相独立抽样的,对于任意的f,上式都是期望 \(\mathbb{E}[f(\mathbf{x})]\) 的无偏估计。 如果样本是独立同分布(i.i.d)的,根据大数定律,当样本数量 \(N \rightarrow \infty\) 时,样本的均值收敛于真实的期望值。
通过选择不同的f,我们可以得到概率分布p的任何感兴趣的信息。
方差 \(f(\mathbf{x})=(\mathbf{x}-\mathbb{E}[\mathbf{x}])^{2}\)
差分熵 \(f(\mathbf{x})=-\log (p(x))\)
\(f(x)=\mathbb{1}_{x>x}\) 可以得到 \(p\left(x>x_{*}\right)\) ,其中 \(x_*\) 是一个参数
所以,如果我们能得到一个联合概率分布 \(p(\mathbf{x})\) 的样本,我们就能探查到这个分布很多信息。
小技巧
可以通过联合概率分布的样本得到边缘概率分布吗?
实际上,如果 \(\mathbf{x}^1,\dots,\mathbf{x}^N\) 是联合概率分布的样本, 那么其中 \(\mathbf{x}^1_i,\dots,\mathbf{x}^N_i\) 就是 \(x_i\) 的边缘概率分布 \(p(x_i)\) 的样本。 因此,如果我们能得到联合概率分布的样本,那么同时也得到了边缘概率分布的样本。
另外我们也有直接从边缘概率分布采样的算法。
15.2. 蒙特卡罗(Monte Carlo)¶
15.3. 马尔科夫链(Markov Chain)¶
一个马尔科夫链是一个随机过程,随着时间的变化”状态”也随之发生变化的过程。我们用 \({X_i}\) 表示状态序列, 状态之间的转化过程是随机的。
(这个公式中状态是离散变量,关于连续变量稍后再讲)
上述公式表明,给定状态序列后,时刻t的状态只与t-1时刻的状态相关,而与更早时刻状态无关(这也被称作马尔科夫性)。 因此,在给定状态序列后,我们可以根据当前的状态确定下一个状态。
马尔科夫链的状态取值集合被称为状态空间,控制着从一状态转移到下一个状态的数值称为 转移核(transition kernel) 或者 转移矩阵(ransition matrix) 。
15.3.1. 一个例子¶
我们假设一个马尔科夫链的状态空间大小为3(有3个不同的状态值),状态之间的转换概率如下图所示, 图中箭头表示从一个状态转移到下一个状态,边上数值表示转移的概率值。 请注意,在这个马尔可夫链中,无论您当前的状态是什么,您都只能前往两种可能的状态,也就是并不是任意两个状态间都能直接转换。
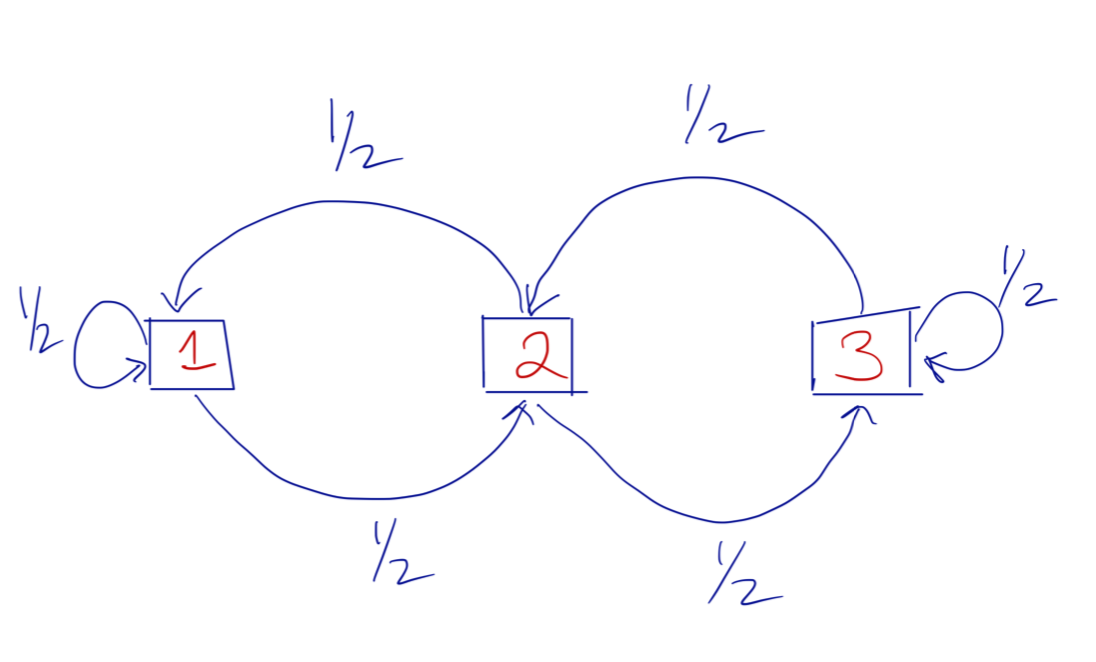
图 15.3.1 状态转换概率图¶
我们也可以用状态转移矩阵来表示状态之间的转换概率。
矩阵的中每个元素 \(P_{ij}\) 表示从状态i转移到状态j的概率,假设n表示马尔科夫链的第n个节点,则有:
从这个状态转移矩阵中可以看到,从状态1转移到状态3的概率是0,因为在矩阵的(1,3)(这里行列索引从1开始计算)位置的元素为0 。
马尔科夫链的第一状态的产生是初始概率决定 \(\boldsymbol{\pi}=[\pi_i],\sum_{\pi_i} = 1\) , \(\pi_i\) 表示链的第一个节点是第i个状态的概率 。这里我们假设 \(\boldsymbol{\pi}=[0,0,1]\) ,也就是链的第一个节点肯定是状态3。
def markov_chain(pi, transition, n):
stats = list(range(1, len(pi) + 1))
s = []
if n < 1:
return s
s.append(np.random.choice(stats, 1, p=pi)[0])
for i in range(n - 1):
p = transition[s[i]-1]
s.append(np.random.choice(stats, 1, p=p)[0])
return s
# 初始概率
pi = [0, 0, 1]
# 状态转移概率矩阵
p = np.asarray([[0.5, 0.5, 0], [0.5, 0, 0.5], [0, 0.5, 0.5]])
# 生成马尔科夫链
chain = markov_chain(pi, p, 5)
print(chain)
>>> [3, 2, 1, 1, 1]
另外我们约定 \(\boldsymbol{\pi}^n\) 表示经过n次转换后(也就是链长为n时),各个状态的概率分布。 注意,这里不是转移概率,而是边缘概率,也就是不管上一个节点状态是什么,下一个状态的概率分布, 其中 \(\boldsymbol{\pi}^0=[0,0,1]\) 。
例如,从状态3开始,经过5次转换后 \(\boldsymbol{\pi}^{5}=(0.3125,0.34375,0.34357)\)
pi = np.asarray([0, 0, 1])
p = np.asarray([[0.5, 0.5, 0], [0.5, 0, 0.5], [0, 0.5, 0.5]])
pi_n = pi
for i in range(5):
print(i,pi_n)
pi_n = pi_n.dot(p)
print(i, pi_n)
>>>0 [0 0 1]
>>>1 [0. 0.5 0.5]
>>>2 [0.25 0.25 0.5 ]
>>>3 [0.25 0.375 0.375]
>>>4 [0.3125 0.3125 0.375 ]
>>>5 [0.3125 0.34375 0.34375]
15.3.2. 时间可逆性(Time Reversibility)¶
满足如下条件的马尔科夫链是 时间可逆(time reversible) 的。
沿着”正向”(时间轴方向)移动的状态序列和沿着”反向”移动的状态序列拥有相同的概率分布。 此外,上面的定义意味着 \(\left(X_{0}, X_{1}\right) \stackrel{D}{=}\left(X_{1}, X_{0}\right)\) , 进一步可得 \(X_{0} \stackrel{D}{=} X_{1}\) 。
因为 \(X_1\) 和 \(X_0\) 拥有相同分布,也就意味着 \(\pi_{1}=\pi_{0}\) 。但是因为 \(\pi_{1}=\pi_{0} P\) , 其中 P 是状态转移矩阵,这就是 \(\pi_{0}\) 就是稳态分布。 综上可得,一个时间可逆的马尔科夫链是一个平稳分布。
除了平稳性,时间可逆的属性还能得出如下等式:
最后一行可以改写成:
这被称为 局部平衡等式(local balance equations) 。一个关键的特性是: 如果转移概率矩阵P和分布 \(\pi\) 拥有局部平衡等式, 那么,\(\pi\) 就是转移矩阵P所控制的马尔科夫链的稳态分布。
备注
为什么这一切都很重要?
时间可逆性与利用马尔可夫链蒙特卡罗的分析相关, 因为它允许我们找到一种方法来构建适当的马尔可夫链,从中进行模拟。 在大多数MCMC应用程序中,我们可以轻松确定最终的稳态分布,因为它通常是由复杂贝叶斯计算产生的后验概率分布, 我们的问题是我们无法模拟计算这个分布。所以问题在于如何构建马尔可夫链,使其平稳分布是我们给定的那个后验概率分布。
重要
时间可逆性为我们提供了一种构建收敛于给定平稳分布的马尔可夫链的方法。 只要我们可以证明具有给定转移矩阵P的马尔可夫链满足关于平稳分布的 局部平衡等式 , 我们就可以知道链将会收敛到稳态分布。
15.3.3. 总结¶
我们想从复杂的概率密度 \(\pi\) 中抽样。
非周期和不可约马尔可夫链最终会收敛到某个稳态分布 \(\pi\)。
如果具有转移矩阵P的马尔可夫链相对于 \(\pi\) 是时间可逆的,那么 \(\pi\) 必须是马尔可夫链的平稳分布。
给定由转移矩阵P控制的马尔科夫链,我们可以模拟它很长一段时间,最终我们将从平稳分布 \(\pi\) 模拟。
这是MCMC技术的基本要点,我在这里给出了最简短的介绍。 也就是说,在下一节中,我们将讨论如何构建一个适当的马尔可夫链来模拟稳态分布。
15.4. Markov Chain Monte Carlo¶
假设我们想从 \(p_{\mathbf{x}}(\mathbf{x})\) 采样, 但是我们只知道 \(p_{\mathbf{x}}\) 正比于一个乘项 (i.e. \(p_{\mathbf{x}}(\mathbf{x})=p_{\mathbf{x}}^{*}(\mathbf{x}) / Z\) , 但是我们只能计算 \(p_{\mathbf{x}}^{*}(\mathbf{x})\) )。 最初,这似乎是一个非常复杂的问题,因为我们不知道Z.
我们的方法是构造一个马尔科夫链(Markov chain) \(\mathbf{P}\) ,另其稳态分布为 \(\pi=p_{\mathbf{x}}\) , 并且我们只需要使用 \(p_{\mathbf{x}}^{*}\) ,而不需要用到Z。 用任意状态 \(\mathbf{x}\) 初始化链的第一个节点,然后执行这个马尔科夫链,直到其收敛到分布 \(\pi=p_{\mathbf{x}}\) , 然后我们就得到了服从分布 \(p_{\mathbf{x}}^{*}\) 的样本 注解 。 这样的采样方法就叫做马尔科夫蒙特卡洛(MCMC,Markov Chain Monte Carlo)法。
备注
马尔科夫链本身就是一个样本点组成的链,当马尔科夫链足够长并且已经收敛到其稳态分布 \(\pi=p_{\mathbf{x}}\) 之后, 再继续产生的后续样本就都是服从概率分布 \(\pi=p_{\mathbf{x}}\) 的。 当然是收敛之后再产生的样本,收敛前样本是不行的。
为了实现这个方法,我们需要回答如下问题:
如何构造这样一个马尔科夫链 \(\mathbf{P}\)
马尔科夫链需要执行多长,才能收敛到稳态分布?
Metropolis-Hastings 算法就是回答第一个问题的方法;对于第二问题,To answer the second, we’ll look at the “mixing time” of Markov chains through Cheeger’s inequality.
15.4.1. Metropolis-Hastings¶
提示
上文我们讲到,一个马尔科夫链可以收敛到一个稳态分布的条件是满足 “detailed balance” ( \(\boldsymbol{\pi}_{i} \mathbf{P}_{i j}=\boldsymbol{\pi}_{j} \mathbf{P}_{j i}\) )。 我们只需要找到这样一个马尔科夫链,并且让其稳态分布是我们想要采样的目标分布 \(p_{\mathbf{x}}\) , 然后执行这个马尔科夫链,经过一定次数的状态转以后,当达到稳态分布后,再产生的样本点就是分布分布的采样点。
而一个马尔科夫链是否能够收敛,与其初始状态无关,只与状态转移矩阵 \(\mathbf{P}\) 相关, 所以我们只需要找到一个合适的 \(\mathbf{P}\) 即可。
我们用 \(\boldsymbol{\pi}=\left[\boldsymbol{\pi}_{i}\right]\) 表示马尔科夫链 \(\mathbf{P}\) 的稳态分布, 并且令其等于我们想要从中采样的目标概率分布 \(p_{\mathbf{x}}\) 。
我们将要构造一个马尔科夫链 \(\mathbf{P}\) ,其状态转移概率矩阵为 \([ \mathbf{P}_{ij}]\) 。
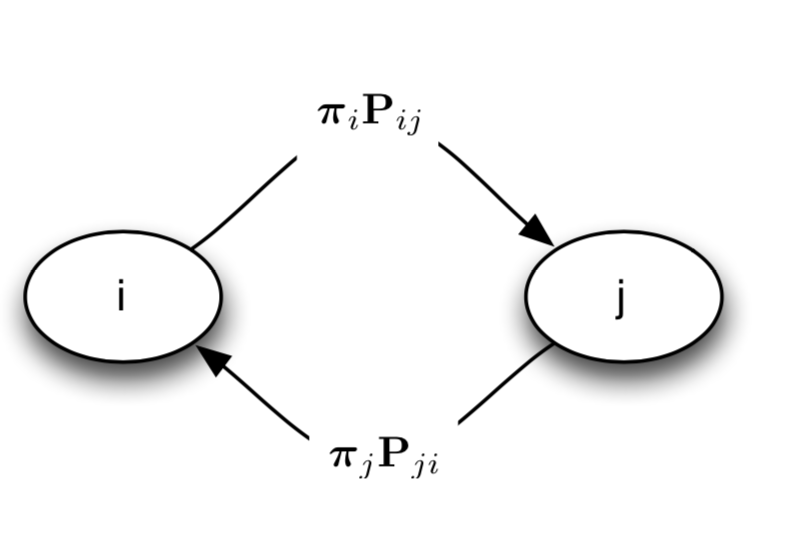
图 15.4.1 图1:马尔科夫链的稳态表示 \(\boldsymbol{\pi}_{i} \mathbf{P}_{i j}=\boldsymbol{\pi}_{j} \mathbf{P}_{j i}\) 。 换句话说就是,从状态i流转到状态j的概率和状态j流转到状态i的概率相同。¶
并且,我们需要 \(\mathbf{P}\) 是一个可逆转的马尔科夫链。
定义1 可逆转马尔科夫链(Reversible Markov chain)
满足如下条件的马尔科夫链被称为可逆马尔可夫链。
This equation is also referred to as detailed balance.
Intuitively, detailed balance says that the probability “flowing” from i to j is the same amount of probability “flowing” from j to i, where by probability “flow” from i to j we mean \(\boldsymbol{\pi}_{i} \mathbf{P}_{i j}\) (i.e. the probability of being in i and transitioning to j).
满足 detailed balance 的 \(\mathbf{\pi}\) 意味着 \(\mathbf{\pi}\) 就是 \(\mathbf{P}\) 的稳态分布。
为了得到一个这样的 \(\mathbf{P}\) ,我们先从一个 “提议(proposed)” 注解 转移矩阵 \(\mathbf{K}\) 开始, 然后通过修改 \(\mathbf{K}\) 去得到我们想要的 \(\mathbf{P}\) 。 \(\mathbf{K}\) 的选取没有太多的限制,可以不必和 \(p_{\mathbf{x}}\) 有关。 我们用一个矩阵 \([\mathbf{K}_{ij}]\) 表示 \(\mathbf{K}\) ,要求:
备注
“提议(proposed)” 状态矩阵的意思就是,先随便选择一个任意的可能不符合要求的转移矩阵。
我们假设 \(\mathbf{P}_{i j}\) 等于 \(\mathbf{K}_{i j}\) 乘以一个因子 \(R(i, j)\) , 使得 “detailed balance”( \(\boldsymbol{\pi}_{i} \mathbf{P}_{i j}=\boldsymbol{\pi}_{j} \mathbf{P}_{j i}\) ) 等式成立。
推导演变过程如下:
那么这个 \(\mathbf{R}\) 是什么才能使等式成立呢?可以这样定义 \(\mathbf{R}_{i j}\) :
注意, \(\mathbf{R}_{i j}\) 和 \(\mathbf{R}_{j i}\) 是i,j互换,直观来看就是分子分母互换, 然后我们把 \(\mathbf{R}\) 带入上述等式:
对于其中的 min函数,我们分情况讨论,我们令 \(\alpha=\frac{\boldsymbol{\pi}_j \mathbf{K}_{j i} }{ \boldsymbol{\pi}_i \mathbf{K}_{i j} }\) , \(\beta=\frac{\boldsymbol{\pi}_i \mathbf{K}_{i j} }{ \boldsymbol{\pi}_j \mathbf{K}_{j i} }\)
如果 \(\boldsymbol{\pi}_j \mathbf{K}_{j i} > \boldsymbol{\pi}_i \mathbf{K}_{i j}\) ,则 \(\alpha >1 , \beta <1\) ,上述等式为:
(15.4.10)¶\[ \begin{align}\begin{aligned}\boldsymbol{\pi}_{i} \mathbf{K}_{i j} \times 1 = \boldsymbol{\pi}_{j} \mathbf{K}_{j i} \frac{\pi_i \mathbf{K}_{i j}}{\pi_j \mathbf{K}_{j i}}\\\boldsymbol{\pi}_{i} \mathbf{K}_{i j} = \boldsymbol{\pi}_{i} \mathbf{K}_{i j} \text{ 等式1成立!}\end{aligned}\end{align} \]
如果 \(\boldsymbol{\pi}_j \mathbf{K}_{j i} < \boldsymbol{\pi}_i \mathbf{K}_{i j}\) ,则 \(\alpha <1 , \beta >1\) ,上述等式为:
(15.4.11)¶\[ \begin{align}\begin{aligned}\boldsymbol{\pi}_{i} \mathbf{K}_{i j} \frac{\boldsymbol{\pi}_j \mathbf{K}_{j i}}{\boldsymbol{\pi}_i \mathbf{K}_{i j}} = \boldsymbol{\pi}_{j} \mathbf{K}_{j i} \times 1\\\boldsymbol{\pi}_{j} \mathbf{K}_{j i} = \boldsymbol{\pi}_{j} \mathbf{K}_{j i} \text{ 等式1成立!}\end{aligned}\end{align} \]
如果 \(\boldsymbol{\pi}_j \mathbf{K}_{j i} = \boldsymbol{\pi}_i \mathbf{K}_{i j}\) ,则 \(\alpha =1 , \beta =1\) ,等式成立。
回顾一下,首先我们有一个离散值的随机变量 \(\mathbf{x}\) ,及其概率分布 \(p_{\mathbf{x}}(\mathbf{x})\) 。 变量 \(\mathbf{x}\) 的取值可以是离散值 \(x_1,x_i,\dots,x_N\) , 现在我们需要从概率分布 \(p_{\mathbf{x}}(\mathbf{x})\) 中进行采样。 我们构造了一个马尔科夫链,其稳态分布是我们的目标分布 \(\boldsymbol{\pi}(i)=p_{\mathbf{x}}(x_i)\) 。 这个马尔科夫链的转移矩阵 \(\mathbf{P}_{ij}\) 是由我们”随便”设置的一个转移矩阵 \(\mathbf{K}_{ij}\) 和一个因子 \(\mathbf{R}(i,j)\) 组成的。其中
备注
前文讲过, \(p_{\mathbf{x}}^*(x_i) =\frac{1}{Z} p_{\mathbf{x}}(x_i)\) ,其中 Z是归一化因子, 在R中需要的仅仅是 \(p_{\mathbf{x}}(x_j)\) 和 \(p_{\mathbf{x}}(x_i)\) 的比值,所以可以去掉Z。
我们称R为接受因子(acceptance ratio)。采样过程如下:
重要
确定我们要采样的目标概率分布 \(p_{\mathbf{x}}(\mathbf{x})\) ,可以是任意分布,比如一个概率图的联合概率分布。
选取一个简单的状态转移矩阵。也就是变量 \(\mathbf{x}\) 从一个取值到另一个取值转移概率分布 \(K(\mathbf{x_j}|\mathbf{x_i})\)。
首先,任意生成一个 \(\mathbf{x}\) 的初始值 \(\mathbf{x}^0\) 。
迭代,利用 \(K(\mathbf{x}^{t}|\mathbf{x}^{t-1})\) 生成 \(\mathbf{x}\) 的一个候选取值 \(\mathbf{x}^{t}\) 。
计算出接受率 \(r=R(\mathbf{x}^{t-1},\mathbf{x}^{t})\)
从一个[0,1]均匀分布中生成一个数字 \(\mu \sim \operatorname{Unif}(0,1)\) 。
如果 \(\mu \le r\) 则接受这个样本 \(\mathbf{x}^{t}\) ;否则不接受。 重复4~7步骤。
当t足够大时,达到收敛状态,再生成的样本就是服从概率分布 \(p_{\mathbf{x}}(\mathbf{x})\) 的样本。
那么”提议分布” \(K(\mathbf{x}_j |\mathbf{x}_i)\) 要如何选取呢?
如果我们能选取一个 对称(symmetric) 的分布 \(K\) , 也就是 \(K(\mathbf{x}_j |\mathbf{x}_i) = K(\mathbf{x}_i |\mathbf{x}_j)\) ,那么接受率R的计算将进一步简化。
当 \(\mathbf{x}\) 是离散变量:
如果变量 \(\mathbf{x}\) 是一个有m个取值的离散随机变量, 那么我们可以定义一个有m个值的均匀分布 \(U \sim \operatorname{Unif}(1,\dots,i,\dots,m)\) , 每个值的取值概率都是 \(\frac{1}{m}\) 。 我们用 \(U_i\) 代表 \(\mathbf(x)_i\) , 从 \(\mathbf(x)_i\) 转移到任意一个状态(取值) 都是等的概率 \(\frac{1}{m}\) 。
(15.4.14)¶\[K( \mathbf{x}_j |\mathbf{x}_i) = U(j) = \frac{1}{m} = U(i) = K( \mathbf{x}_i |\mathbf{x}_j)\]或者是,我们定义一个[0,1] 的均匀分布 \(U \sim \operatorname{Unif}(0,1)\) ,然后将区间[0,1]分成m份, 分别和 \(\mathbf(x)_i\) 对应。
当 \(\mathbf{x}\) 是连续变量:
我们定义一个均值为0的正态分布 \(g(\varepsilon) = Normal(0,\sigma^2)\) ,令
(15.4.15)¶\[\mathbf{x}^{t} = \mathbf{x}^{t-1} + \varepsilon\]由于均值为0的正态分布是对称的,所以 \(g(\varepsilon) = g(-\varepsilon)\) ,则有
(15.4.16)¶\[ \begin{align}\begin{aligned}\mathbf{x}^{t} &= \mathbf{x}^{t-1} + \varepsilon\\\mathbf{x}^{t-1} &= \mathbf{x}^{t} - \varepsilon\\K(i,j) = g(\varepsilon) &= g(-\varepsilon) = K(j,i)\end{aligned}\end{align} \]
Metropolis-Hastings算法的缺陷!
重要
Metropolis-Hastings算法的缺陷!
我们仔细观察下接受率R,如果 \(p_{\mathbf{x}}^* (x_j)\) 比 \(p_{\mathbf{x}}^*(x_i)\) 小很多,那么这个R就会很小, 也就是 很难从低概率的状态转移到高概率的状态
15.4.2. 例子:正态分布的采样¶
15.4.3. 多变量采样¶
多变量问题
如果概率分布是多个变量的联合概率分布 \(p_{\mathbf{x}} = p(\mathbf{x}_1,\dots,\mathbf{x}_n)\) , 或者 \(\mathbf{x}\) 是一个n为向量。 标准的Metropolis算法,再一次迭代时同时更新所有变量
15.4.3.1. Block-wise Sampling¶
15.4.3.2. Component-wise Sampling¶
15.4.4. Gibbs 采样¶
https://theclevermachine.wordpress.com/2012/11/05/mcmc-the-gibbs-sampler/